Μαθηματικά Γ' Λυκείου

24 / 368

23
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
27. Απόδειξη
( ) ( ) ( )
= - òβ
α
E Ω f x g x dx
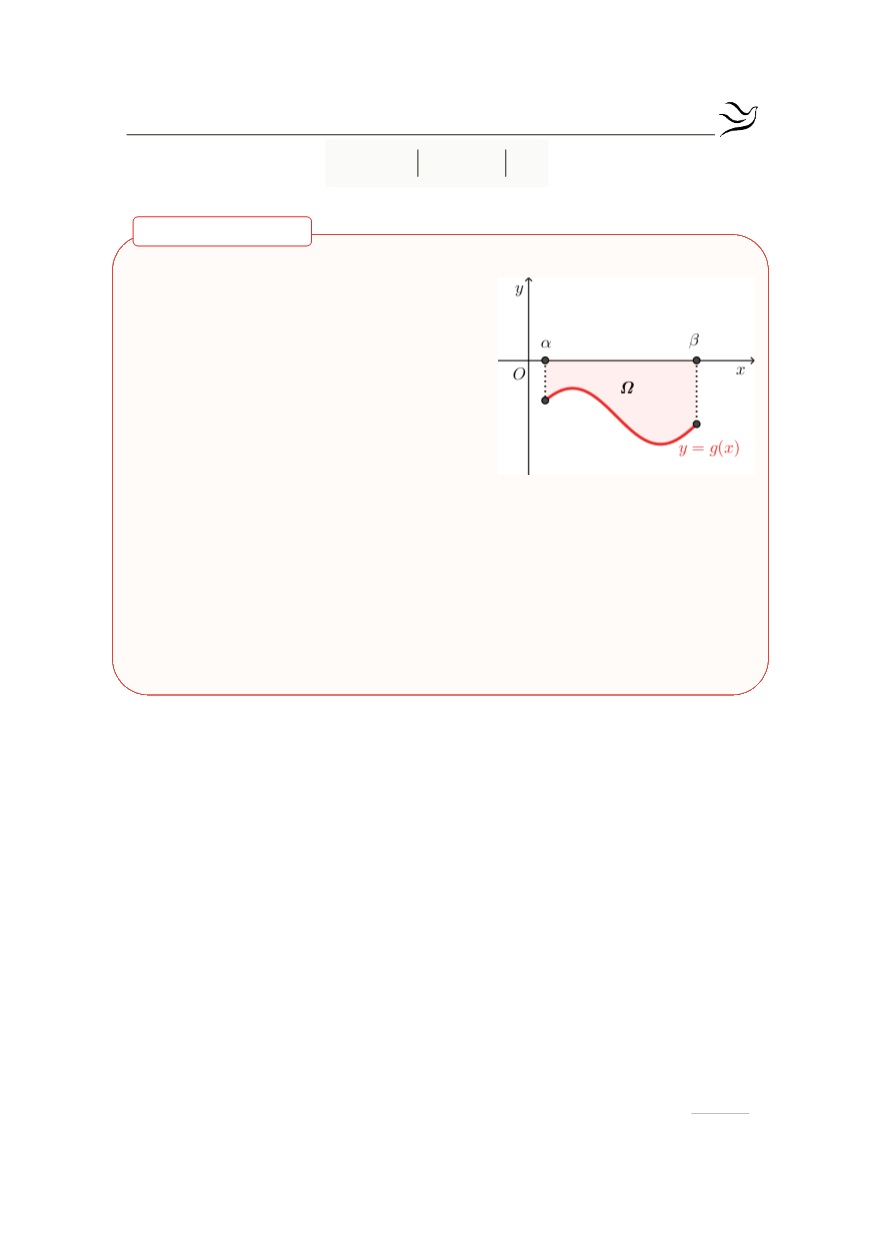
Εμβαδόν μεταξύ
g C και x΄x , ( )
g x 0£
Με τη βοήθεια του τύπου
( ) ( ) ( ) ( )
= - ò β
α
E Ω f x g x dx μπορούμε να υπο-
λογίσουμε το εμβαδόν του χωρίου Ω που
περικλείεται από τον άξονα x x¢ , τη γραφική
παράσταση μιας συνάρτησης g, με ( ) £
g x 0
για κάθε [ ]
Î
x α,β και τις ευθείες x α = και
x β = . Πράγματι, επειδή ο άξονας x x¢ είναι η
γραφική παράσταση της συνάρτησης ( ) =
f x 0 , έχουμε
( ) ( ) ( ) ( )
= - ò β
α
E Ω f x g x dx ( ) ( )
= é- ù = -ë û ò ò β β
α α
g x dx g x dx .
Επομένως, αν για μια συνάρτηση g ισχύει g(x) 0£ για κάθε x [α,β] Î , τότε
( ) ( )
= -òβ
α
E Ω g x dx