Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
22
26
. Απόδειξη
Επομένως , έχουμε:
( ) ( )
( )
(
)
( )
(
)
( ) ( )
(
)
é
ù
¢
= =
+ - + =
-
ë
û
ò
ò
β
β
α
α
Ε Ω Ε Ω f x c g x c dx f x g x dx
.
Άρα,
( )
( ) ( )
(
)
=
-
ò
β
α
E
Ω f x g x dx
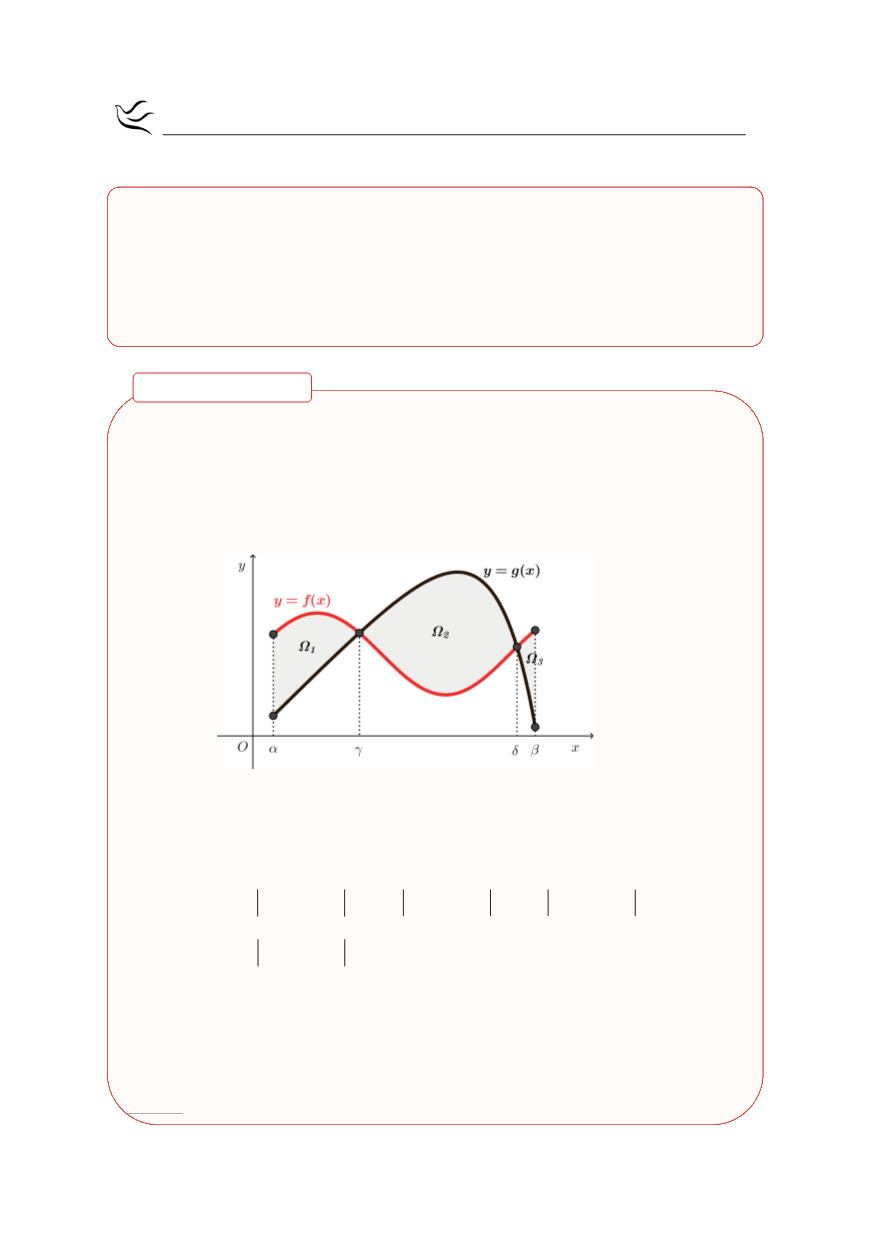
Εμβαδόν μεταξύ
f
C
και
g
C
Αν η διαφορά
( ) ( )
-
f x g x
δεν διατηρεί σταθερό πρόσημο στο
[ ]
α,β
, τότε το
εμβαδόν του χωρίου Ω που περικλείεται από τις γραφικές παραστάσεις των
f,g
και τις ευθείες
x
α
=
και
x
β
=
είναι ίσο με το άθροισμα των εμβαδών των
χωρίων
1 2
Ω ,Ω
και
3
Ω
. Δηλαδή,
( ) ( ) ( ) ( )
= + +
1
2
3
Ε Ω Ε Ω Ε Ω Ε Ω
( ) ( )
(
)
=
-
ò
γ
α
f x g x dx
( ) ( )
(
)
( ) ( )
(
)
+
-
+
-
ò
ò
δ
β
γ
δ
g x f x dx f x g x dx
( ) ( )
=
-
ò
γ
α
f x g x dx
( ) ( )
( ) ( )
+
-
+
-
ò
ò
δ
β
γ
δ
f x g x dx f x g x dx
( ) ( )
=
-
ò
β
α
f x g x dx
Επομένως,









