17
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
20
. Απόδειξη
( )
( ) ( )
0
0
0
x x
0
f x f x
f x lim
0
x x
-
®
-
¢
=
³
-
( )
2
P
αν
(
)
0 0
x x ,x
δ
Î +
, τότε, λόγω της
( )
1
, θα είναι
( ) ( )
0
0
f x f x
0
x x
-
£
-
, οπότε
θα έχουμε
( )
( ) ( )
0
0
0
x x
0
f x f x
f x lim
0
x x
+
®
-
¢
=
£
-
.
( )
3
Έτσι, από τις
( )
2
και
( )
3
έχουμε
( )
0
f x 0
¢
=
.
Η απόδειξη για τοπικό ελάχιστο είναι ανάλογη.
Κριτήριο Τοπικών Ακροτάτων
Έστω μια συνάρτηση f παραγωγίσιμη σ’ ένα διάστημα
( )
α,β
, με εξαίρεση
ίσως ένα σημείο του
0
x
, στο οποίο όμως η f είναι
συνεχής
.
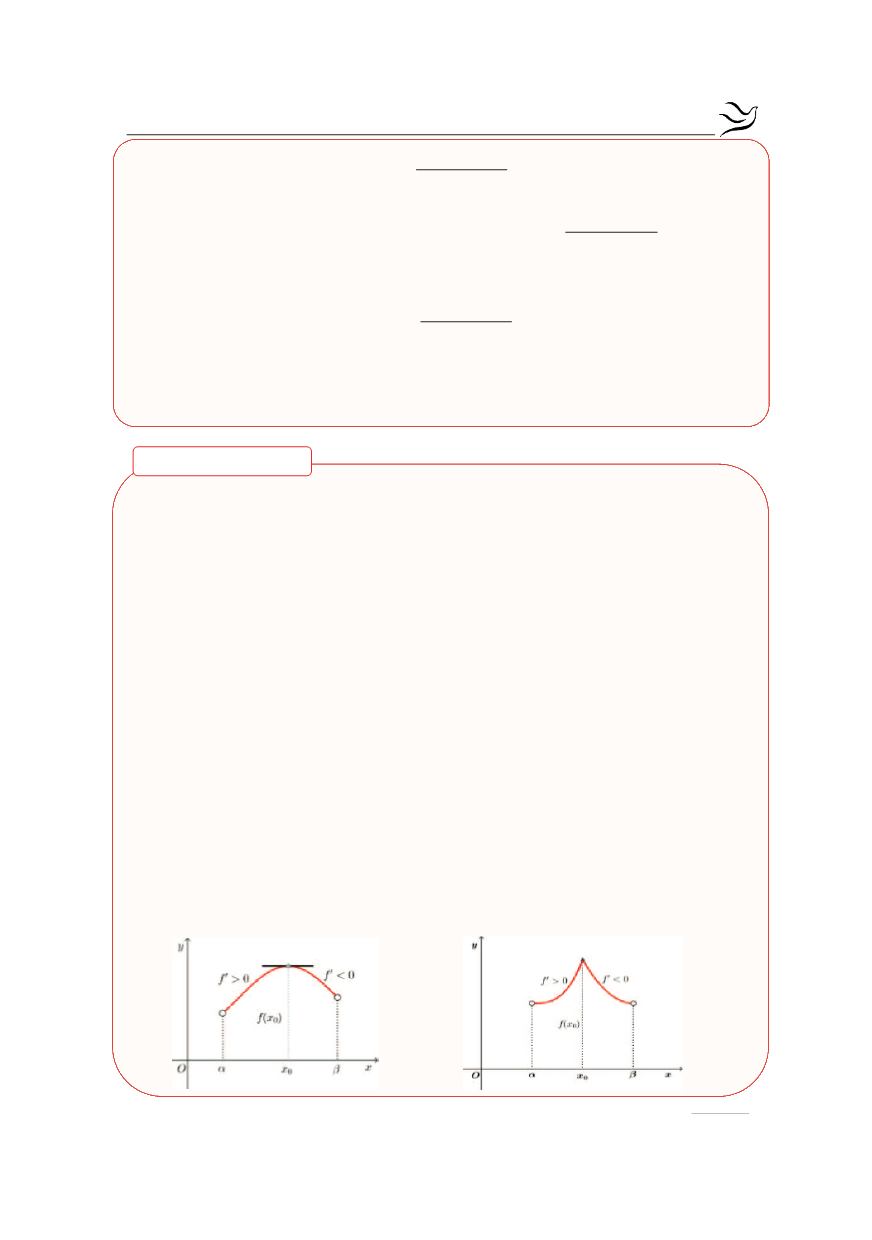
i)
Αν
( )
f x 0
¢
>
στο
(
)
0
α,x
και
( )
f x 0
¢
<
στο
(
)
0
x ,
β
, τότε το
( )
0
f x
είναι τοπικό
μέγιστο της f.
ii)
Αν
( )
f x 0
¢
<
στο
(
)
0
α,x
και
( )
f x 0
¢
>
στο
(
)
0
x ,
β
, τότε το
( )
0
f x
είναι τοπικό
ελάχιστο της f.
Απόδειξη
i)
Επειδή
( )
f x 0
¢
>
για κάθε
(
)
0
x
α,x
Î
και η f είναι συνεχής στο
0
x
, η f είναι
γνησίως αύξουσα στο
(
]
0
α,x
. Έτσι έχουμε
( ) ( )
0
f x f x
£
, για κάθε
(
]
0
x
α,x
Î
.
( )
1
Επειδή
( )
f x 0
¢
<
για κάθε
(
)
0
x x ,
β
Î
και η f είναι συνεχής στο
0
x
, η f είναι
γνησίως φθίνουσα στο
[
)
0
x ,
β
. Έτσι έχουμε
( ) ( )
0
f x f x
£
, για κάθε
[
)
0
x ,
β
.
( )
2









