Μαθηματικά Γ' Λυκείου

15 / 368

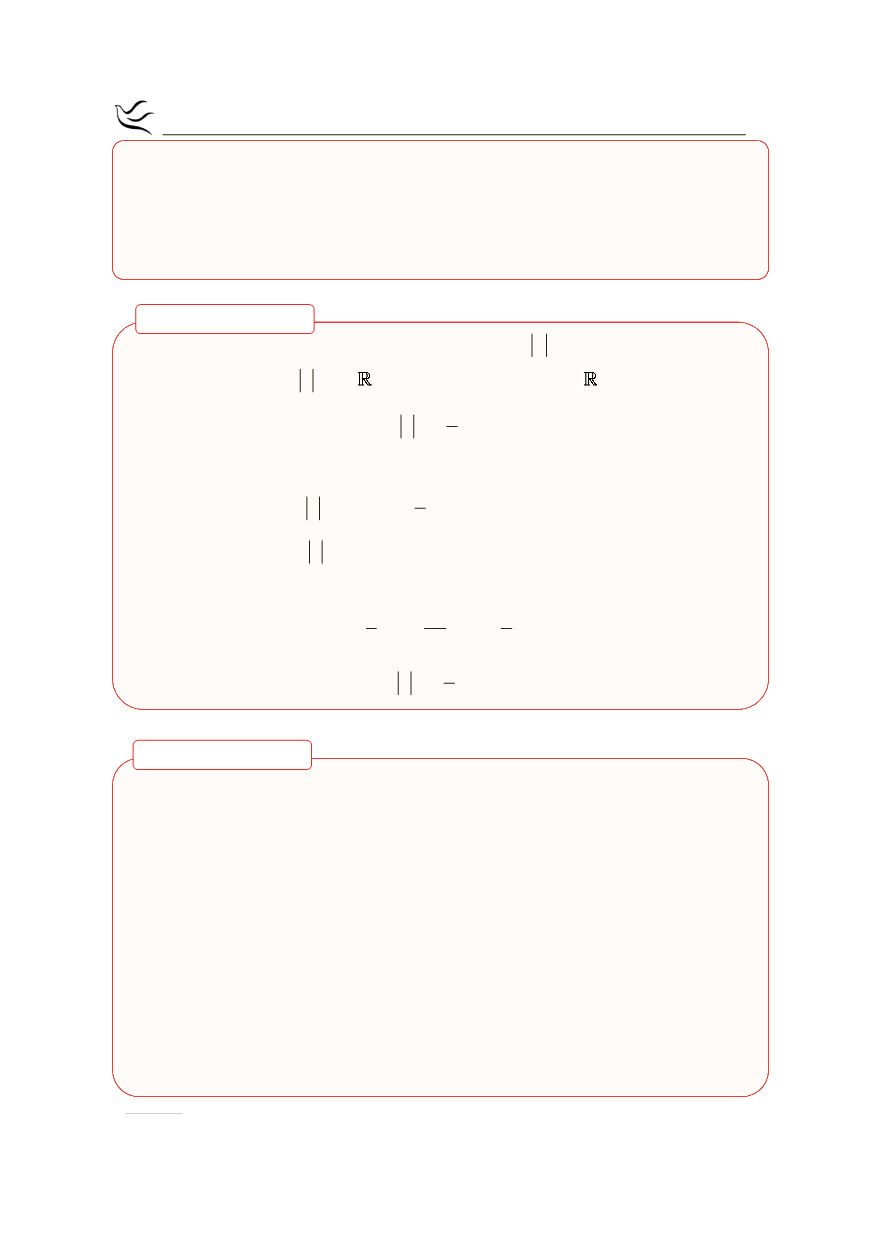
Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
14
15. Απόδειξη
16. Απόδειξη
Απόδειξη
Αν x xlnα
y α e = = θέτουμε u x ln α = , οπότε u
y e= .
Άρα,
( )u u xlnα x
y e e u e lnα α lnα
¢
¢ ¢ = = × = × = .
Παράγωγος της ( )
f x = ln x
Η συνάρτηση ( )
f x ln x= , *
xÎ είναι παραγωγίσιμη στο * και ισχύει
( ) 1
ln x
x
¢ =
Απόδειξη
P Αν x 0> , τότε ( ) ( ) 1
ln x lnx
x
¢ ¢
= = ,
P Αν x 0< , τότε ( )
ln x ln x= - , οπότε, αν θέσουμε ( )
y ln x= - και u x=- ,
έχουμε y lnu= .
Επομένως, ( ) ( ) 1 1 1
y lnu u 1
u x x
¢
¢ ¢ = = × = - =
-
και άρα
( ) 1
ln x
x
¢ = .
Σταθερή Συνάρτηση
Έστω μια συνάρτηση f ορισμένη σε ένα διάστημα Δ. Αν
P η f είναι συνεχής στο Δ και
P ( )
f x 0¢ = για κάθε εσωτερικό σημείο x του Δ
τότε η f είναι σταθερή σε όλο το διάστημα Δ.
Απόδειξη
Αρκεί να αποδείξουμε ότι για οποιαδήποτε 1 2 x ,x Δ Î ισχύει ( ) ( )1 2 f x f x= .
Πράγματι
P Αν 1 2 x x= , τότε προφανώς ( ) ( )1 2 f x f x= .
P Αν 1 2 x x< , τότε στο διάστημα [ ]
1 2 x ,x η f ικανοποιεί τις υποθέσεις του θε-
ωρήματος μέσης τιμής.