Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
16
19
. Απόδειξη
Έστω
1 2
x ,x
Δ
Î
με
1
2
x x
<
. Θα δείξουμε ότι
( ) ( )
1
2
f x f x
<
.
Πράγματι, στο διάστημα
[
]
1 2
x ,x
η f ικανοποιεί τις προϋποθέσεις του Θ.Μ.Τ.
Επομένως, υπάρχει
(
)
1 2
ξ x ,x
Î
τέτοιο, ώστε
( ) ( ) ( )
2
1
2 1
f x f x
f
ξ
x x
-
¢
=
-
, οπότε έχου-
με
( ) ( ) ( )(
)
2
1
2 1
f x f x f
ξ x x
¢
- =
-
.
Επειδή
( )
f
ξ 0
¢
>
και
2 1
x x 0
- >
, έχουμε
( ) ( )
2
1
f x f x 0
- >
, οπότε
( ) ( )
1
2
f x f x
<
.
Στην περίπτωση που είναι
( )
f x 0
¢
<
εργαζόμαστε αναλόγως.
Θεώρημα
Fermat
Έστω μια συνάρτηση f ορισμένη σ’ ένα διάστημα Δ και
0
x
ένα
εσωτερικό
ση-
μείο του Δ. Αν η f παρουσιάζει
τοπικό ακρότατο
στο
0
x
και είναι
παραγωγί-
σιμη
στο σημείο αυτό, τότε:
( )
0
f x 0
¢
=
Απόδειξη
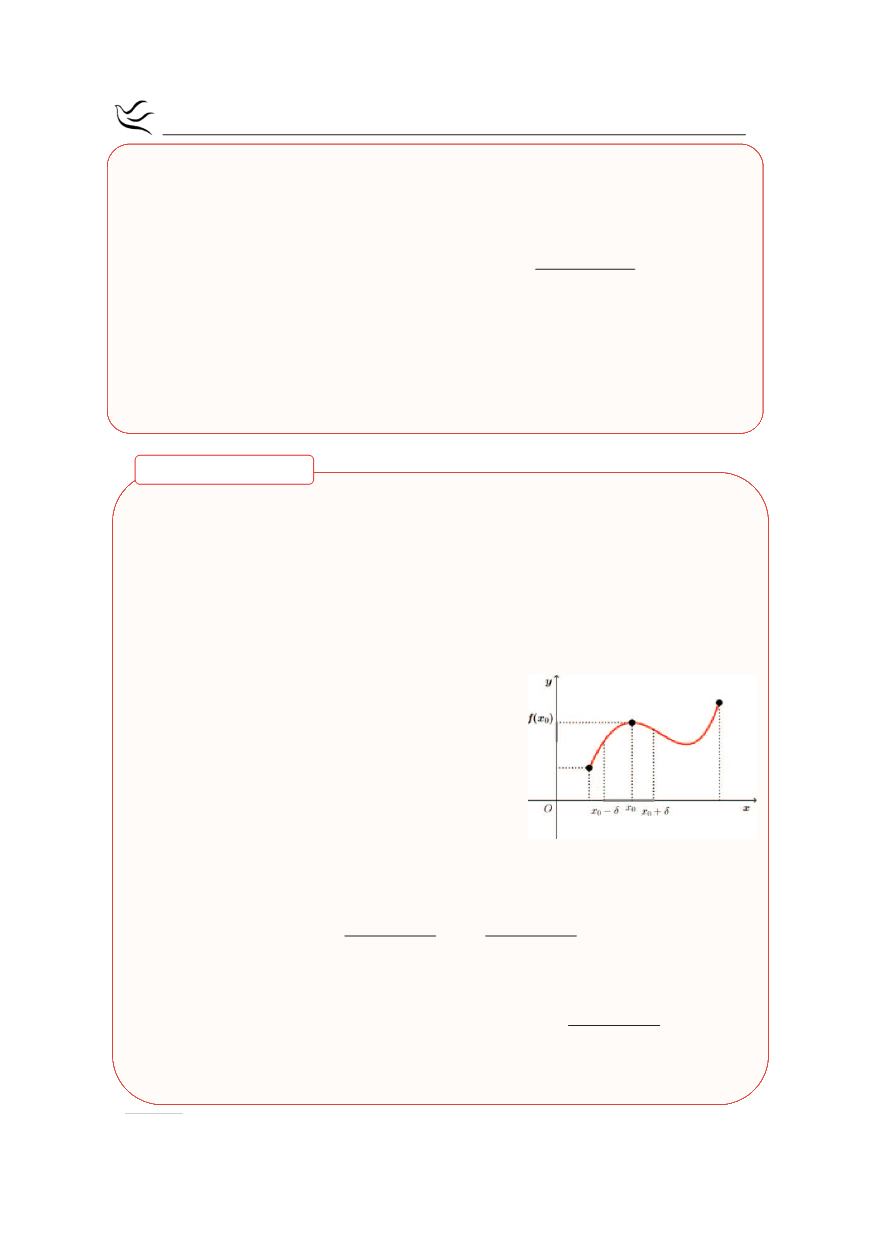
Ας υποθέσουμε ότι η f παρουσιάζει στο
0
x
το-
πικό μέγιστο. Επειδή το
0
x
είναι εσωτερικό ση-
μείο του Δ και η f παρουσιάζει σ’ αυτό τοπικό
μέγιστο, υπάρχει
δ 0
>
τέτοιο, ώστε
(
)
0
0
x
δ,x δ Δ
- + Í
και
( ) ( )
0
f x f x
£
, για κάθε
(
)
0
0
x x
δ,x δ
Î - +
. (1)
Επειδή, επιπλέον, η f είναι παραγωγίσιμη στο
0
x
, ισχύει
( )
( ) ( )
( ) ( )
0
0
0
0
0
x x
x x
0
0
f x f x
f x f x
f x lim
lim
x x
x x
-
+
®
®
-
-
¢
=
=
-
-
.
Επομένως,
P
αν
(
)
0
0
x x
δ,x
Î -
, τότε, λόγω της
( )
1
, θα είναι
( ) ( )
0
0
f x f x
0
x x
-
³
-
, οπότε
θα έχουμε









