11
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
9. Απόδειξη
Απόδειξη
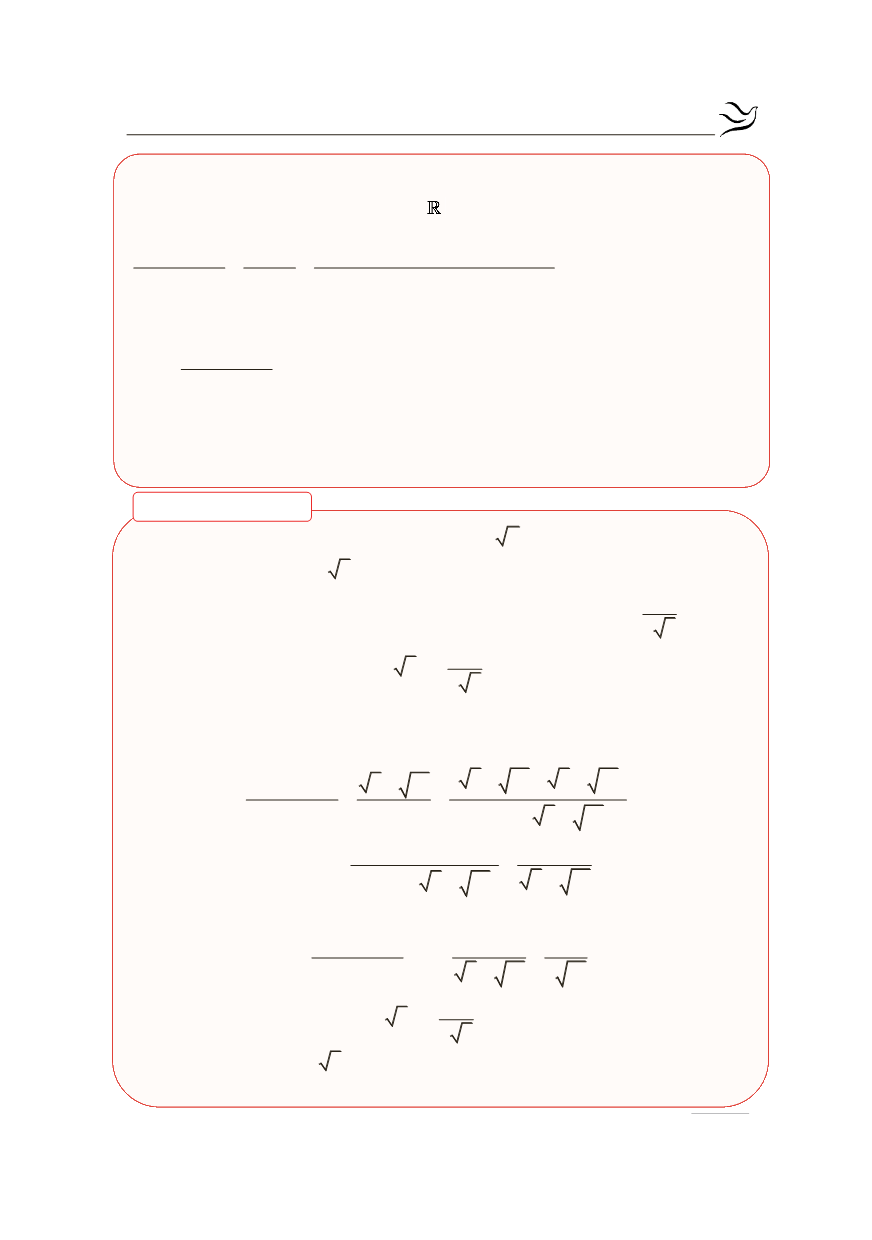
Πράγματι, αν
0
x
είναι ένα σημείο του , τότε για
0
x x
¹
ισχύει:
( ) ( )
(
)
(
)
ν 1 ν 2
ν 1
ν
ν
0
0
0
0
ν 1 ν 2
ν 1
0
0
0
0
0
0
x x x x x ... x
f x f x x x
x x x ... x
x x
x x
x x
-
-
-
-
-
-
-
+ + +
-
-
=
=
= + + +
-
-
-
,
οπότε
( ) ( )
(
)
0
0
0
ν 1 ν 2
ν 1
ν 1 ν 1
ν 1
ν 1
0
0
0
0
0
0
x x
x x
0
f x f x
lim
lim x x x ... x
x x ... x
νx
x x
-
-
-
-
-
-
-
®
®
-
=
+ + + = + + + =
-
,
δηλαδή
( )
ν
ν 1
x
νx
-
¢ =
.
Παράγωγος της
( )
f x = x , x 0
>
Έστω η συνάρτηση
( )
f x x
=
.
Η συνάρτηση f είναι παραγωγίσιμη στο
(
)
0,
+¥
και ισχύει
( )
1
f x
2 x
¢
=
, δηλαδή
( )
1
x
2 x
¢
=
.
Απόδειξη
Πράγματι, αν
0
x
είναι ένα σημείο του
(
)
0,
+¥
, τότε για
0
x x
¹
ισχύει:
( ) ( )
(
)(
)
(
)
(
)
-
+
-
-
=
=
-
-
-
+
0
0
0
0
0
0
0
0
x x x x
x x
f x f x
x x
x x
x x x x
(
)
(
)
-
=
=
+
-
+
0
0
0
0
x x
1
x x
x x x x
οπότε
( ) ( )
0
0
0
x x
x x
0
0
0
f x f x
1
1
lim
lim
x x
x x 2 x
®
®
-
=
=
-
+
,
δηλαδή
( )
1
x
2 x
¢
=
.
Προκύπτει πως η
( )
f x x
=
δεν είναι παραγωγίσιμη στο 0.









