7
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
2. Απόδειξη
1.
Απόδειξη
Αποδείξεις
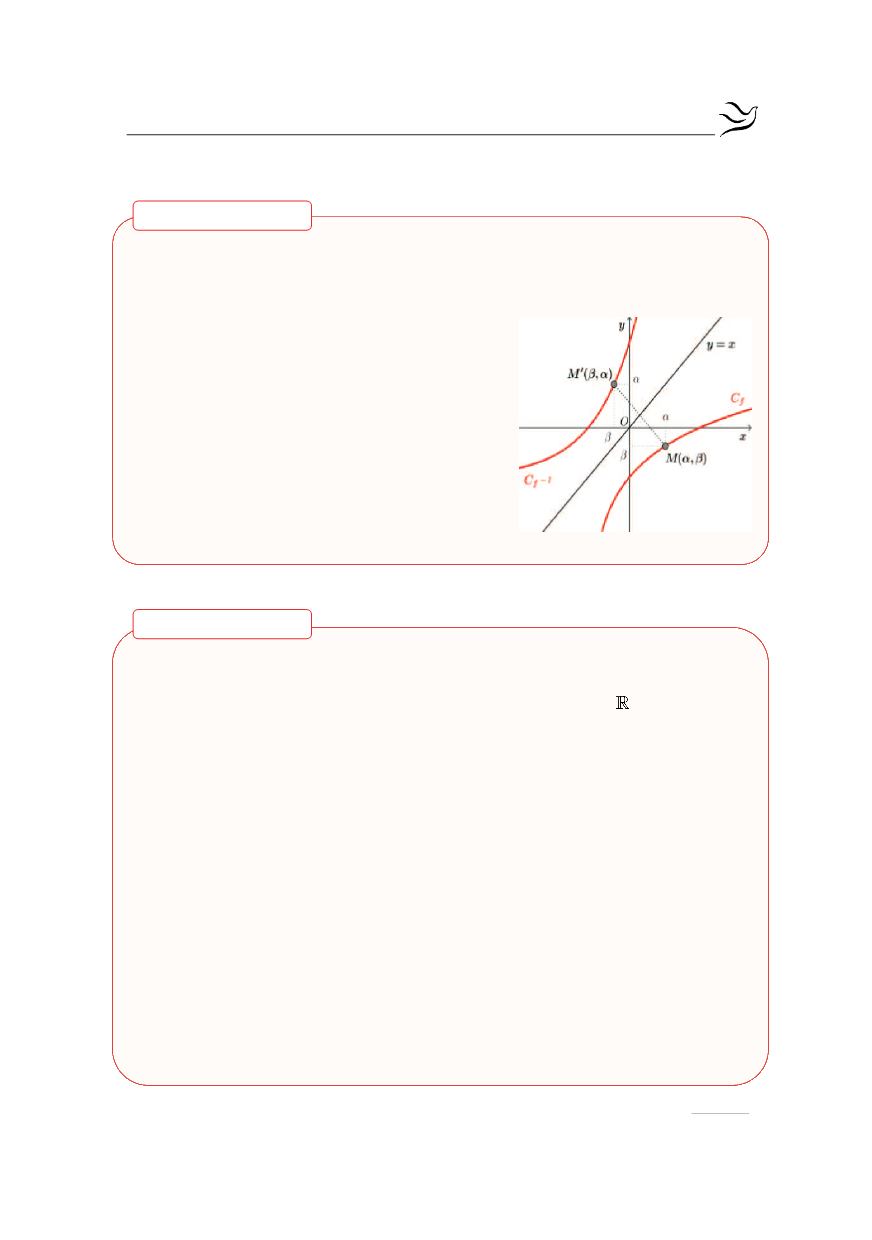
Γραφική Παράσταση Αντίστροφης
Έστω
f
συνάρτηση
1 1
-
με αντίστροφη την
1
f
-
.
Επειδή
ισχύει
( )
( )
1
f x y f y x
-
= Û =
αν ένα σημείο
( )
M
α,β
ανήκει στη γραφική πα-
ράσταση C της
f
, τότε το σημείο
( )
Μ β,α
¢
θα
ανήκει στη γραφική παράσταση
C
¢
της
1
f
-
και
αντιστρόφως. Γνωρίζουμε όμως,
πως τα σημεία
αυτά είναι συμμετρικά ως προς την ευθεία που
διχοτομεί τις γωνίες
xOy
και
x Oy
¢ ¢
.
Όριο πολυωνυμικής συνάρτησης
Για το πολυώνυμο
( )
ν
ν 1
ν
ν 1
1
0
P x
α x α x ... α x α
-
-
= +
+ + +
με
0
x
Î
ισχύει ότι
:
( ) ( )
0
0
x x
limP x P x
®
=
Απόδειξη
Είναι :
( )
(
)
0
0
ν
ν 1
ν
ν 1
0
x x
x x
limP x lim
α x α x ... α
-
-
®
®
=
+
+ +
(
)
(
)
0
0
0
ν
ν 1
ν
ν 1
0
x x
x x
x x
lim
α x lim α x
... lim α
-
-
®
®
®
=
+
+ +
0
0
0
ν
ν 1
ν
ν 1
0
x x
x x
x x
α lim x α lim x ... limα
-
-
®
®
®
=
+
+ +
( )
ν
ν 1
ν 0
ν 1 0
0
0
α x α x ... α P x
-
-
= +
+ + =









