13
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
13. Απόδειξη
12. Απόδειξη
14
. Απόδειξη
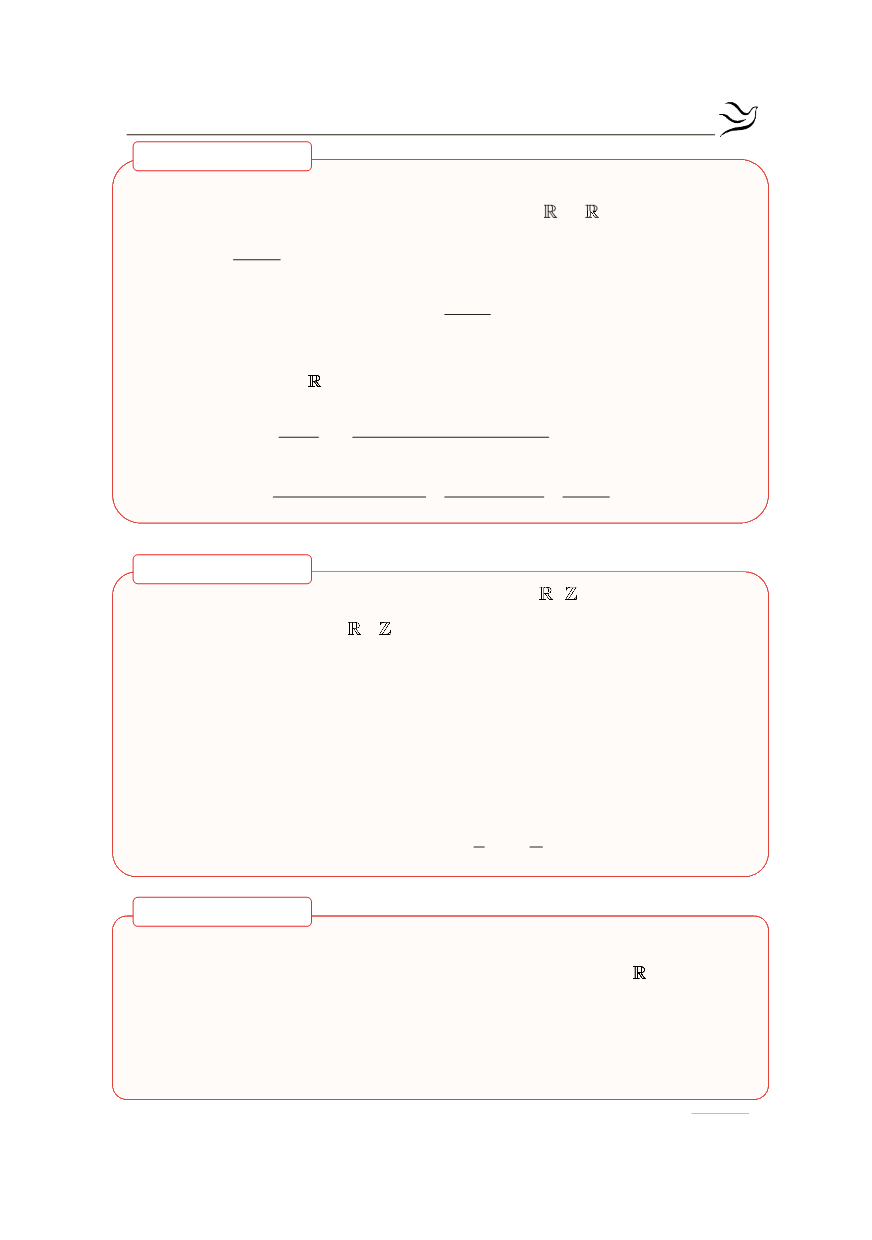
Παράγωγος της
( )
f x =
εφx
Η συνάρτηση
( )
f x
εφx
=
είναι παραγωγίσιμη στο
{
}
1
x /
συνx 0
= -
=
και
ισχύει
( )
2
1
f x
συν x
¢
=
, δηλαδή
(
)
2
1
εφx
συν x
¢ =
.
Απόδειξη
Πράγματι, για κάθε
1
x
Î
έχουμε:
( )
( )
(
)
¢
¢
¢
-
æ
ö
¢ =
=
ç
÷
è
ø
2
ημx συνx ημx συνx
ημx
εφx
συνx
συν x
2
2
2
2
2
συνxσυνx ημxημx συν x ημ x 1
συν x
συν x
συν x
+
+
=
=
=
.
Παράγωγος της
( )
,
Î
α
f x = x
α -
Η συνάρτηση
( )
α
f x x
=
,
α
Î -
είναι παραγωγίσιμη στο
(
)
0,
+¥
και ισχύει
( )
α 1
f x
αx
-
¢
=
, δηλαδή
( )
α
α 1
x
αx
-
¢ =
.
Απόδειξη
Πράγματι, αν
α αlnx
y x e
= =
και θέσουμε
u
αlnx
=
, τότε έχουμε
u
y e
=
.
Επομένως,
( )
u
u
αlnx
α
α 1
1
α
y e e u e
α x
αx
x
x
-
¢
¢
¢
= = × = × × = × =
.
Παράγωγος της
( )
x
f x =
α
Η συνάρτηση
( )
x
f x
α
=
,
α 0
>
είναι παραγωγίσιμη στο
και ισχύει
( )
x
f x
α lnα
¢
=
, δηλαδή
( )
x
x
α α lnα
¢ =
.









