9
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
5. Απόδειξη
P
η g είναι συνεχής στο
[ ]
α,β
και
P
( ) ( )
g
α g β 0
<
,
Αφού
( ) ( )
g
α f α η 0
= - <
( ) ( )
g
β f β η 0
= - >
.
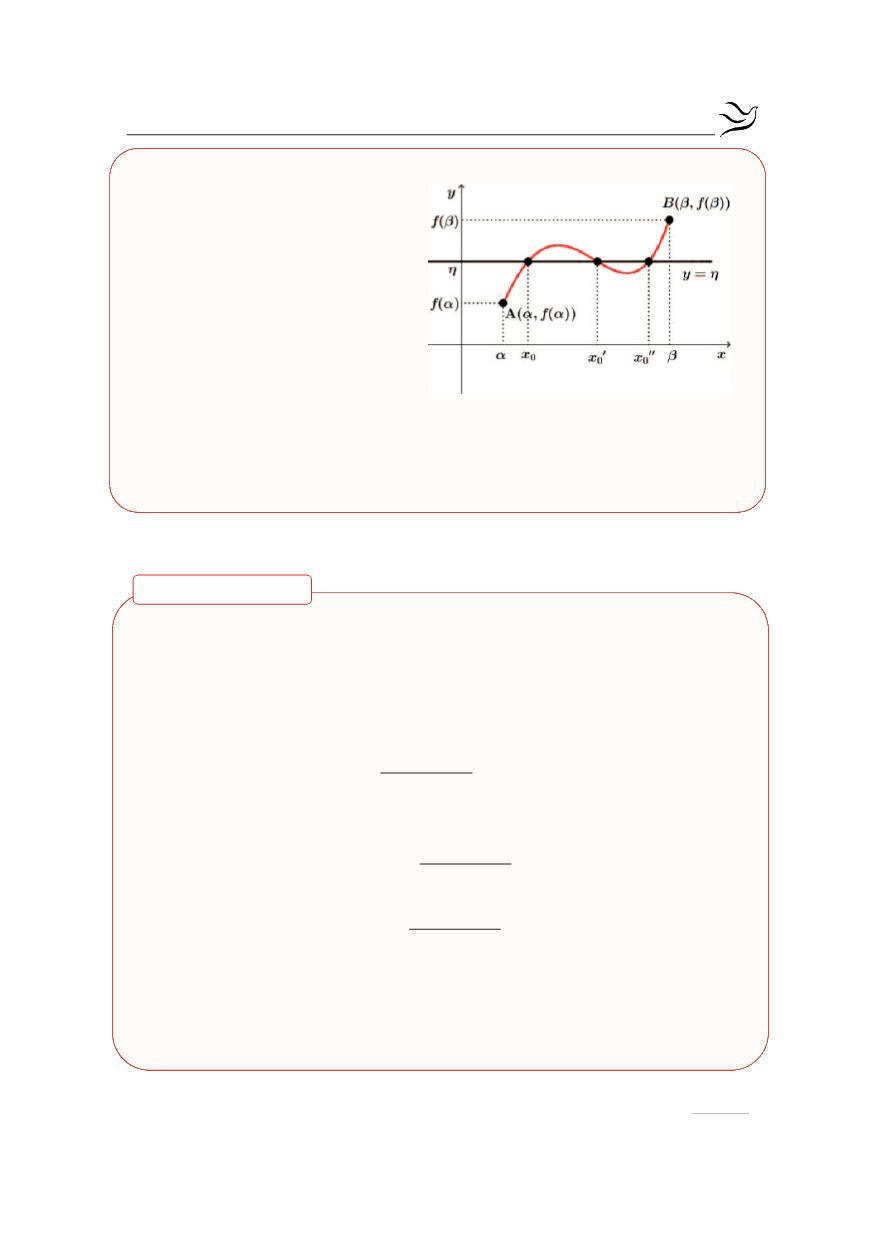
Επομένως, σύμφωνα με το θεώρημα του Bolzano, υπάρχει
( )
0
x
α,β
Î
τέτοιο,
ώστε
( ) ( )
0
0
g x f x
η 0
= - =
, οπότε
( )
0
f x
η
=
.
Παράγωγος και συνέχεια
Αν μια συνάρτηση f είναι παραγωγίσιμη σ’ ένα σημείο
0
x
, τότε είναι και συνε-
χής στο σημείο αυτό.
Απόδειξη
Για
0
x x
¹
έχουμε
:
( ) ( ) ( ) ( ) (
)
0
0
0
0
f x f x
f x f x
x x
x x
-
- =
× -
-
.
Οπότε
( ) ( )
( ) ( ) (
)
0
0
0
0
0
x x
x x
0
f x f x
lim f x f x
lim
x x
x x
®
®
é
-
ù
é - ù =
× -
ê
ú
ë
û
- ë
û
( ) ( )
(
)
0
0
0
0
x x
x x
0
f x f x
lim
lim x x
x x
®
®
-
=
×
-
-
( )
0
f x 0 0
¢= × =
αφού η f είναι παραγωγίσιμη στο
0
x
.
Επομένως,
( ) ( )
0
0
x x
lim f x f x
®
=
, δηλαδή η f είναι συνεχής στο
0
x
.









