Μαθηματικά Γ' Λυκείου

22 / 368

21
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
25. Απόδειξη
Παρατηρούμε ότι
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
= - = - = - ò ò ò β β β
1 2
α α α
Ε Ω Ε Ω Ε Ω f x dx g x dx f x g x dx .
Επομένως,
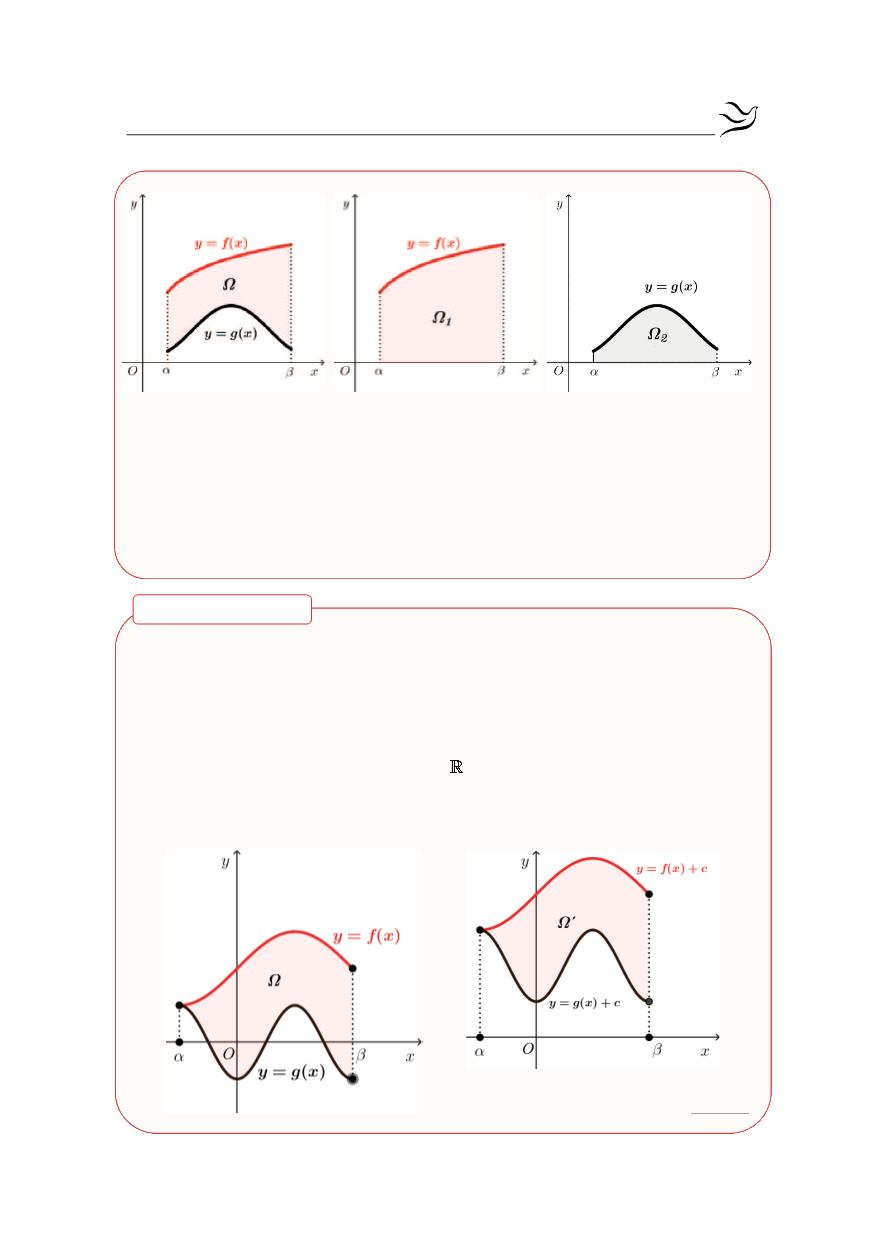
Εμβαδόν μεταξύ
f C και
g C
Έστω δυο συναρτήσεις f και g, συνεχείς στο διάστημα [ ]α,β με ( ) ( )
f x g x³ για
κάθε [ ]
Î
x α,β και Ω το χωρίο που περικλείεται από τις γραφικές παραστάσεις
των f, g και τις ευθείες x α = και x β = . Eπειδή οι συναρτήσεις f,g είναι συνε-
χείς στο [ ]α,β , θα υπάρχει αριθμός c Î τέτοιος ώστε ( ) ( )
+ ³ + ³
f x c g x c 0 ,
για κάθε [ ]
Î
x α,β . Είναι φανερό ότι το χωρίο Ω έχει το ίδιο εμβαδόν με το χω-
ρίο Ω¢ .
( ) ( ) ( ) ( )
= - ò β
α
E Ω f x g x dx