Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
40
41
. Ορισμός
Ορισμένο Ολοκλήρωμα
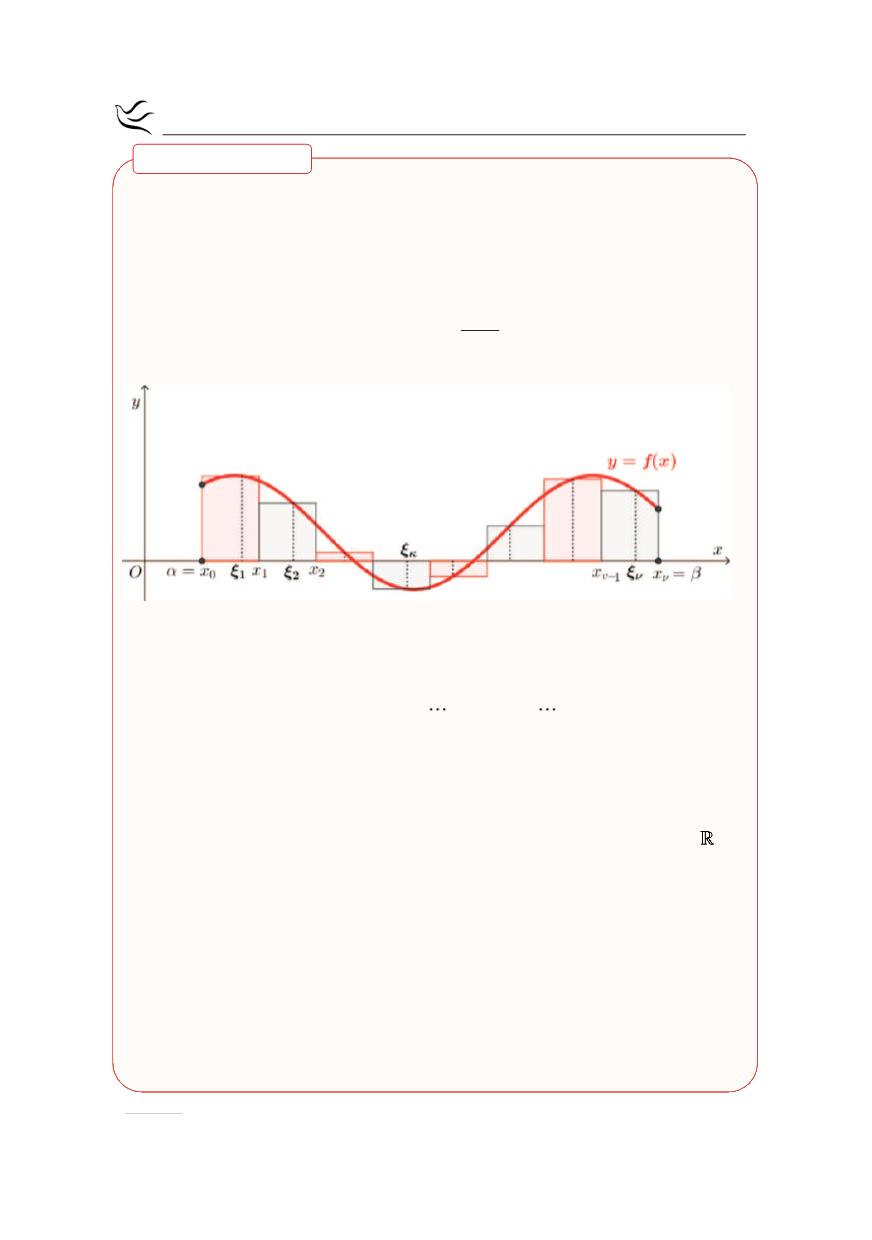
Θεωρούμε συνεχή συνάρτηση f στο
[ ]
α,β
. Χωρίζουμε το διάστημα
[ ]
α,β
με
τα σημεία
0 1 2
ν
α x x x ... x β
= < < < < =
σε ν ισομήκη υποδιαστήματα μήκους
β α
Δx
ν
-
=
.
Στη συνέχεια επιλέγουμε αυθαίρετα ένα
[
]
-
Î
κ
κ 1 κ
ξ x ,x
, για κάθε
{
}
Î
κ 1,2,...,ν
,
και σχηματίζουμε το άθροισμα
( )
( )
( )
( )
=
+
+ +
+ +
ν
1
2
κ
ν
S f
ξ Δx f ξ Δx
f ξ Δx
f ξ Δx
το οποίο συμβολίζεται
( )
=
=
å
ν
ν
κ
κ 1
S
f
ξ Δx
.
Αποδεικνύεται ότι,
“Το όριο του αθροίσματος
ν
S
, δηλαδή το
( )
®¥
=
æ
ö
ç
÷
è
ø
å
ν
κ
ν
κ 1
lim f
ξ Δx
υπάρχει στο
και
είναι ανεξάρτητο από την επιλογή των ενδιάμεσων σημείων
κ
ξ
”.
Το
( )
®¥
=
æ
ö
ç
÷
è
ø
å
ν
κ
ν
κ 1
lim f
ξ Δx
ονομάζεται
ορισμένο ολοκλήρωμα
της συνεχούς συνάρ-
τησης f από το α στο β, συμβολίζεται με
( )
β
α
f x dx
ò
και διαβάζεται “ολοκλή-
ρωμα της f από το α στο β”. Δηλαδή,
( )
( )
ν
β
κ
α
ν
κ 1
f x dx lim f
ξ Δx
®¥
=
æ
ö
= ç
÷
è
ø
å
ò









