Μαθηματικά Γ' Λυκείου

47 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
46
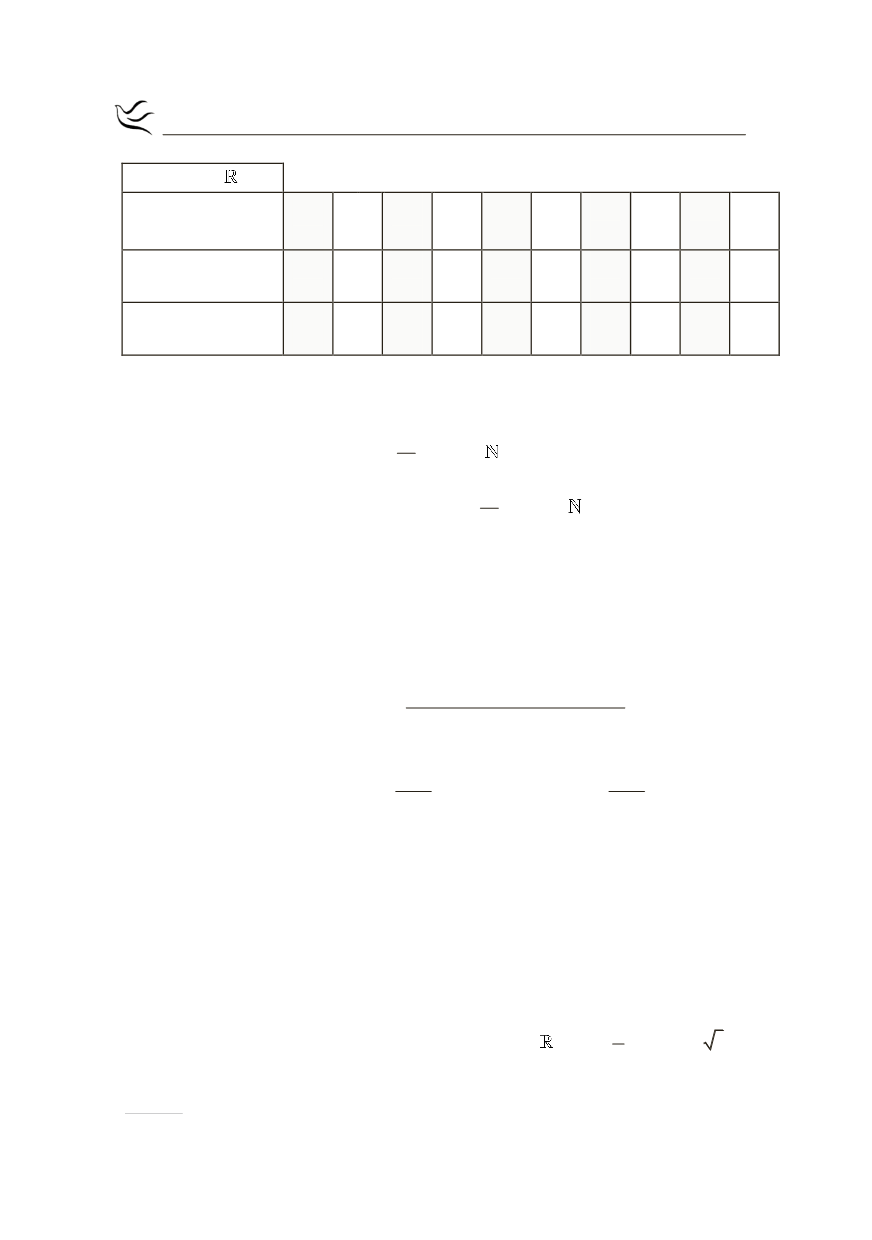
ΘΕΩΡΗΜΑ 2ο (όριο γινομένου)
Αν στο 0 x Î
το όριο της f εί-
ναι:
α 0> α 0< α 0> α 0< 0 0 +¥ +¥ -¥ -¥
και το όριο της g
είναι:
+¥ +¥ -¥ -¥ +¥ -¥ +¥ -¥ +¥ -¥
τότε το όριο της
f ·g είναι:
+¥ -¥ -¥ +¥ ; ; +¥ -¥ -¥ +¥
P Για τον υπολογισμό του ορίου στο +¥ ή -¥ ενός μεγάλου αριθμού συ-
ναρτήσεων χρειαζόμαστε τα παρακάτω βασικά όρια:
Ø
®+¥
= +¥
ν
x
lim x και
®+¥
=
ν
x
1
lim 0
x
, *
vÎ
Ø
®-¥
+¥ì
= í
-¥î
ν
x
, v άρτιος
lim x
, v περιττός
και
®-¥
=
ν
x
1
lim 0
x
, *
vÎ .
P Για την πολυωνυμική συνάρτηση ( ) ν ν 1
ν ν 1 0 P x α x α x ... α-
- = + + + , με ν α 0¹
ισχύει:
( ) ( )
ν
ν
x x
lim P x lim α x
®+¥ ®+¥
= και ( ) ( )
ν
ν
x x
lim P x lim α x
®-¥ ®-¥
=
P Για τη ρητή συνάρτηση
ν ν 1
ν ν 1 1 0
κ κ 1
κ κ 1 1 0
α x α x ... α x α
f(x)
β x β x ... β x β
-
-
-
-
+ + + +
=
+ + + +
, ν α 0¹ , κ β 0¹
ισχύει:
( )
ν
ν
κ
x x
κ
α x
lim f x lim
β x ®+¥ ®+¥
æ ö
= ç ÷
è ø
και ( )
ν
ν
κ
x x
κ
α x
lim f x lim
β x ®-¥ ®-¥
æ ö
= ç ÷
è ø
P Για το όριο εκθετικής - λογαριθμικής συνάρτησης ισχύει ότι
· Αν α 1> , τότε x
x
lim α 0
®-¥
= και x
x
lim α
®+¥
= +¥
α
x 0
limlog x
®
= -¥ και α
x
lim log x
®+¥
= +¥
· Αν 0 α 1 < < , τότε x
x
lim α
®-¥
= +¥ και x
x
lim α 0
®+¥
=
P Αν οι συναρτήσεις f και g είναι συνεχείς στο o x , τότε είναι συνεχείς στο
o x και οι συναρτήσεις: f g+ , c f× , όπου c Î , f g× ,
f
g
, |f| και ν f με
την προϋπόθεση ότι ορίζονται σε ένα διάστημα που περιέχει το o x .