Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
52
P
Ιδιότητες του ολοκληρώματος
( )
β
α
f x dx
ò
.
Ø
( )
( )
β
α
α
β
x
x
f dx
f dx
= -
ò
ò
Ø
( )
α
α
x
f dx 0
=
ò
Ø
Αν
( )
x
f
0
³
για κάθε
[ ]
x
α,β
Î
και
f
συνεχής στο διάστημα αυτό, τό-
τε
( )
β
α
x
f dx 0
³
ò
.
Ø
Έστω
f, g
σ υ ν ε χ ε ί ς συναρτήσεις στο
[ ]
α,β
και
λ,μ
Î
.
Τότε ισχύουν:
·
( )
( )
β
β
α
α
x
x
λf dx λ f dx
=
ò
ò
·
( ) ( )
(
)
( )
( )
β
β
β
α
α
α
f x g x
x
x
dx f dx g dx
+
=
+
ò
ò
ò
και γενικά
·
( )
( )
(
)
( )
( )
β
β
β
α
α
α
λf x μg x
x
x
dx
λ f dx μ g dx
+
=
+
ò
ò
ò
Ø
Αν η f είναι σ υ ν ε χ ή ς σε διάστημα Δ
και
α, β, γ Δ
Î
, τότε ισχύει
( )
( )
( )
β
γ
β
α
α
γ
x
x
x
f dx f dx f dx
=
+
ò
ò
ò
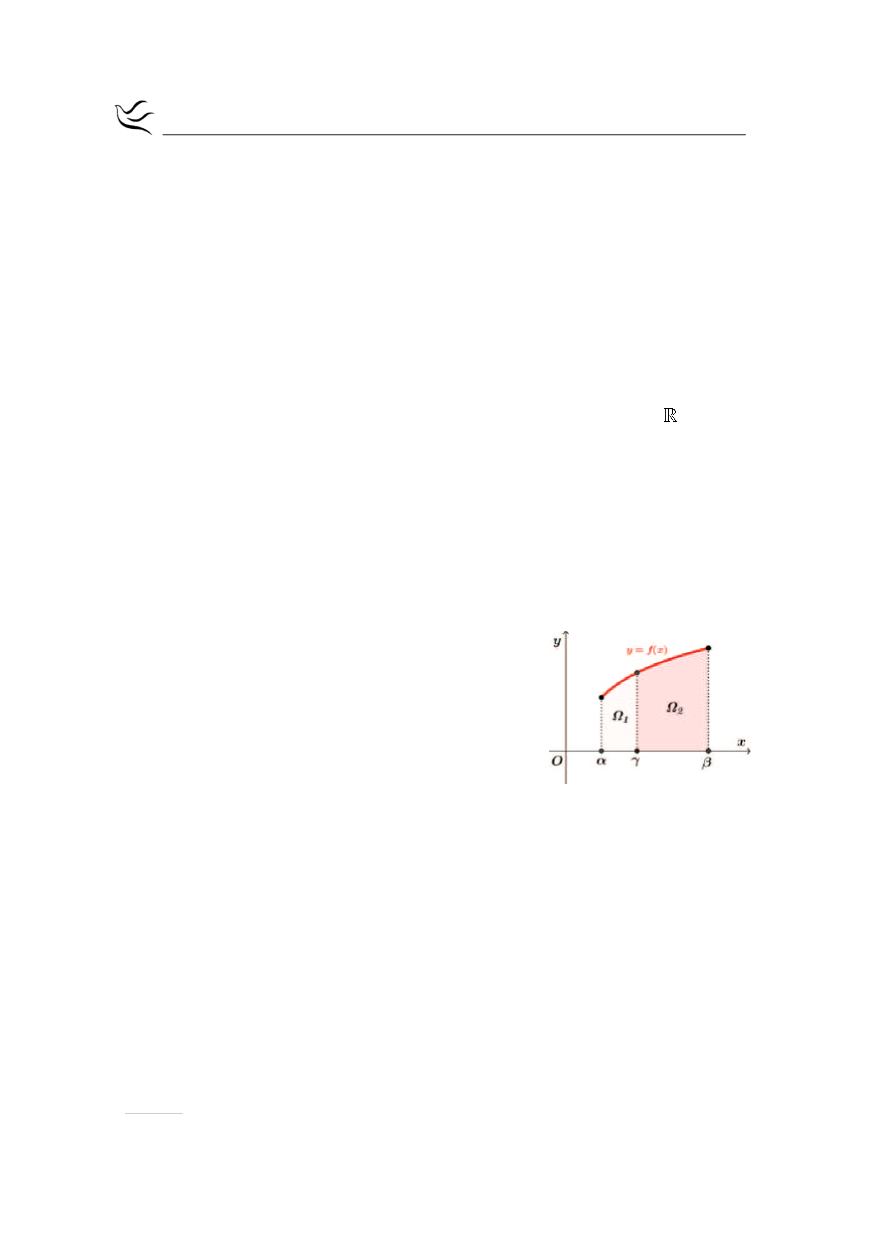
Σημείωση:
Αν
( )
f x 0
³
και
α γ β
< <
η
παραπάνω ιδιότητα δηλώ-
νει
ότι:
( ) ( ) ( )
1
2
Ε Ω Ε Ω Ε Ω
= +
Ø
Έστω f μια σ υ ν ε χ ή ς συνάρτηση σε ένα διάστημα
[ ]
α,β
. Αν
( )
f x 0
³
για κάθε
[ ]
x
α,β
Î
και η συνάρτηση f δεν είναι παντού μη-
δέν στο διάστημα αυτό, τότε
( )
β
α
x
f dx 0
>
ò
.
P
Το
( )
β
α
f x dx
ò
είναι ίσο με το άθροισμα των εμβαδών των χωρίων που
βρίσκονται πάνω από τον άξονα
x x
¢
μείον το άθροισμα των εμβαδών
των χωρίων που βρίσκονται κάτω από τον άξονα
x x
¢
.









