Μαθηματικά Γ' Λυκείου

48 / 368

47
Πρσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
P Οι συναρτήσεις ( )
f x εφx = και ( )
g x σφx = είναι συνεχείς ως πηλίκα συνε-
χών συναρτήσεων.
P Αν η συνάρτηση f είναι συνεχής στο 0 x και η συνάρτηση g είναι συνεχής
στο ( )0 f x , τότε η σύνθεσή τους g f είναι συνεχής στο 0 x .
P Αν μια συνάρτηση f είναι συνεχής σε ένα διάστημα Δ και δε μηδενίζεται
σ’ αυτό, τότε αυτή ή είναι θετική για κάθε f,g ή είναι αρνητική για κάθε
x Δ Î , δηλαδή διατηρεί πρόσημο στο διάστημα Δ.
P Μια συνεχής συνάρτηση f διατηρεί πρόσημο σε καθένα από το διαστή-
ματα στα οποία οι διαδοχικές ρίζες της f χωρίζουν το πεδίο ορισμού της.
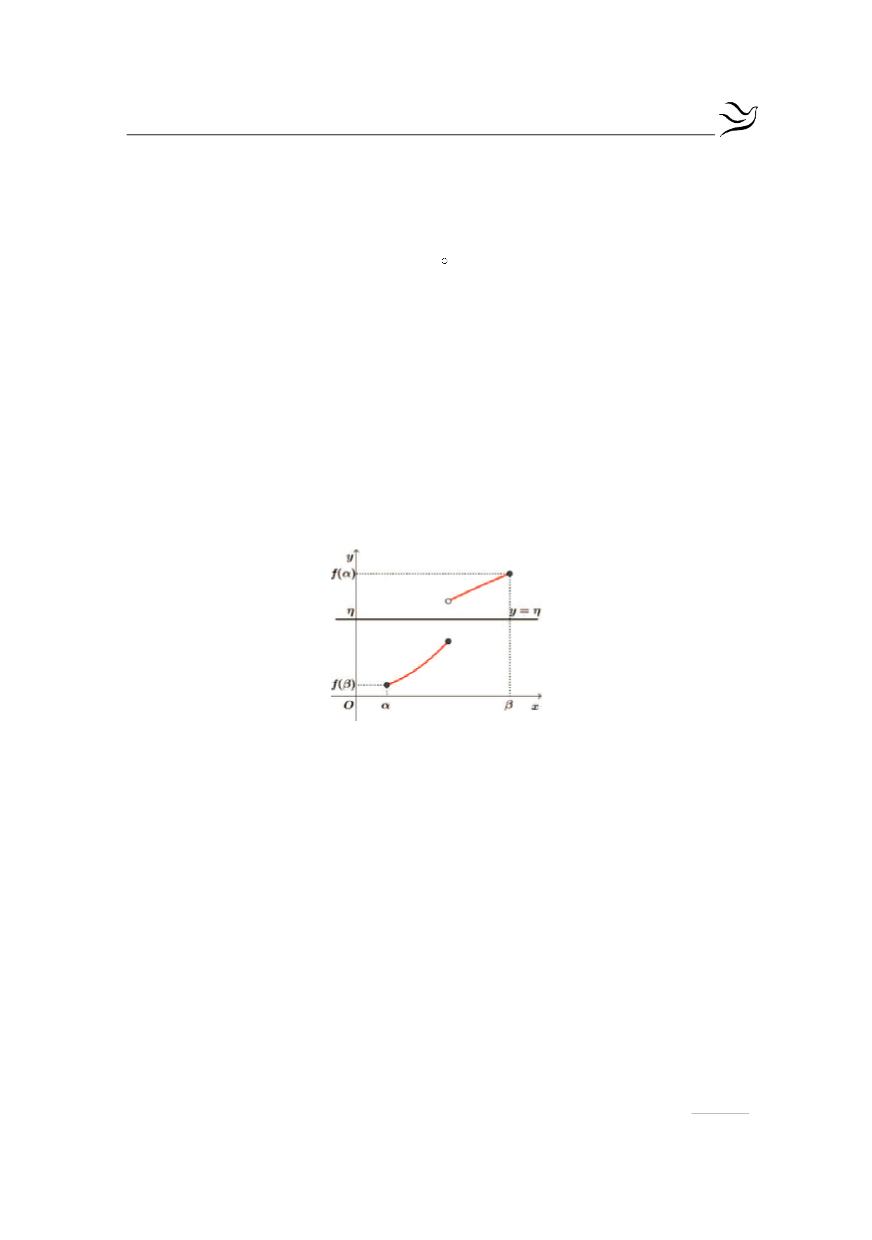
P Αν μια συνάρτηση f δεν είναι συνεχής στο διάστημα [ ]α,β , τότε, όπως
φαίνεται και στο παρακάτω σχήμα, δεν παίρνει υποχρεωτικά όλες τις εν-
διάμεσες τιμές.
P Η εικόνα ( )
f Δ ενός διαστήματος Δ μέσω μιας συνεχούς και μη σταθερής
συνάρτησης f είναι διάστημα.
P Aν μια συνάρτηση f είναι γνησίως αύξουσα και συνεχής σε ένα ανοικτό
διάστημα ( )α,β , τότε το σύνολο τιμών της στο διάστημα αυτό είναι το
διάστημα ( )Α,Β , όπου ( )
x α
Α lim f x
+
®
= και ( )
x β
B lim f x
-
®
= .
P Αν, όμως, η f είναι γνησίως φθίνουσα και συνεχής στο ( )α,β , τότε το σύ-
νολο τιμών της στο διάστημα αυτό είναι το διάστημα ( )Β,Α .
P Από το θεώρημα Μέγιστης και ελάχιστης τιμής και το θεώρημα ενδιά-
μεσων τιμών προκύπτει ότι το σύνολο τιμών μιας συνεχούς συνάρτησης f