Μαθηματικά Γ' Λυκείου

46 / 368

45
Πρσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Ø Αν ( )
0 x x
lim f x
®
= +¥ , τότε ( )
f x 0> κοντά στο o x , ενώ αν ( )
0 x x
lim f x
®
= -¥ ,
τότε ( )
f x 0< κοντά στο o x .
Ø Αν ( )
0 x x
lim f x
®
= +¥ , τότε ( ) ( )
®
- = -¥
0 x x
lim f x , ενώ αν ( )
0 x x
lim f x
®
= -¥ , τό-
τε ( ) ( )
®
- = +¥
0 x x
lim f x .
Ø Αν ( )
0 x x
lim f x
®
= +¥ ή -¥ , τότε ( )
0 x x
1
lim 0
f x ®
= .
Ø Αν ( )
0 x x
lim f x 0
®
= και ( )
f x 0> κοντά στο o x , τότε ( )
0 x x
1
lim
f x ®
= +¥ ,
ενώ αν ( )
0 x x
lim f x 0
®
= και ( )
f x 0> κοντά στο o x , τότε ( )
0 x x
1
lim
f x ®
= -¥ .
Ø Αν ( )
0 x x
lim f x
®
= +¥ ή -¥ , τότε ( )
0 x x
lim f x
®
= +¥ .
Ø Αν ( )
0 x x
lim f x
®
= +¥ , τότε ( )
0
κ
x x
lim f x
®
= +¥ .
Ø i) 2 ν
x 0
1
lim
x ®
= +¥ , *
vÎ .
ii) 2ν 1
x 0
1
lim
x + +
®
= +¥ , vÎ και 2ν 1
x 0
1
lim
x - +
®
= -¥ , v Î .
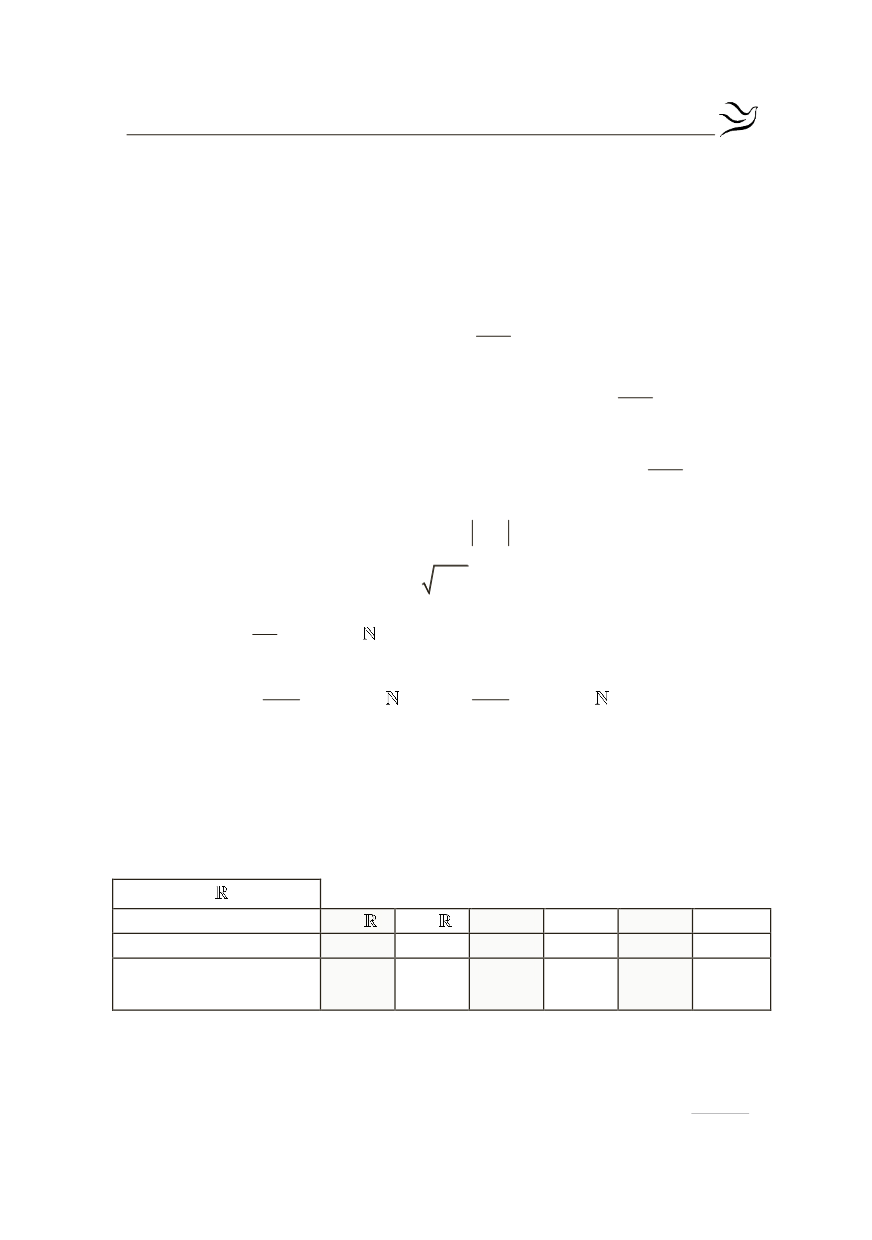
Ø Για το άθροισμα και το γινόμενο ισχύουν τα παρακάτω θεωρήματα:
ΘΕΩΡΗΜΑ 1ο (όριο αθροίσματος)
Αν στο 0 x Î
το όριο της f είναι: α Î α Î +¥ -¥ +¥ -¥
και το όριο της g είναι: +¥ -¥ +¥ -¥ -¥ +¥
τότε το όριο της f g+
είναι:
+¥ -¥ +¥ -¥ ; ;