Απαντήσεις – Υποδείξεις
356
Θέμα 55
α.
Παραγωγίστε τη δοθείσα σχέση.
β.
( )
( ) ( )
(
)
(
)
( )
( )
(
)
+ + +
=
+
x
x
2
e f x f x 1 1 e f x
f x
1 f x
.
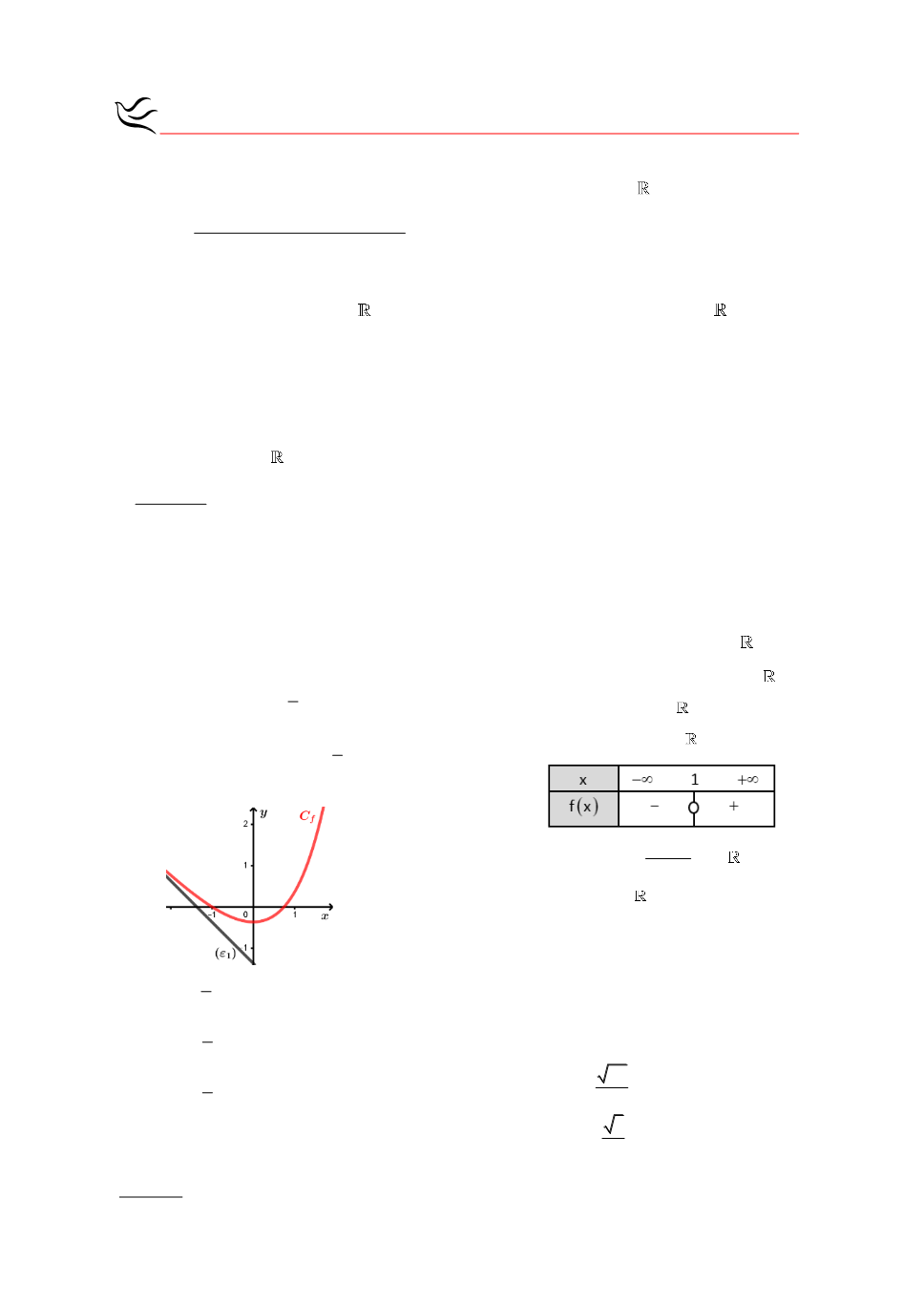
γ.
= +
y x 1
.
δ.
Είναι
( )
+
f x x 1
για κάθε
x
με την
ισότητα να ισχύει μόνο για
=
x 0
.
ε.
Θ.Μ.Τ. στο
1,2
για την
( )
( )
=
2
h x f x
.
Θέμα 56
α.
Είναι
(
)
(
)
+ =
f 0,
.
β.
+ −
2
e 2e 3
2
γ.
0 και 0.
δ.
( )
( )
= − −
y t
2α t 2
Θέμα 57
α.
Θεωρήστε
( )
−
=
1
x
0
c f x e dx
β.
Είναι
(
)
(
)
+ = − +
1
f 0,
,
e
.
γ.
Στο
−
είναι η
= − − −
1
y x 1
e
.
δ.
ε.
Για
−
1
α
e
:
αδύνατη
Για
= −
1
α
e
:
1 ρίζα
Για
−
1
α
e
:
2 ρίζες
Θέμα 58
Α. α.
Παραγωγίστε τη δοθείσα σχέση.
β.
Δείξτε αρχικά ότι η f είναι γνησίως
αύξουσα στο
.
Β. α.
(
= −
1
στο Δ
,0
3
,
)
= +
2
στο Δ 0,
4
Σημείο καμπής το
( )
Ο 0,0
β.
=
y x
Γ.
Είναι
( )
f x x
,
για κάθε
x
Θέμα 59
α.
( )
= −
2
Ε x 10x 2x
,
( )
x 0,5
.
β.
( )
= −
P x 20 2x
,
( )
x 0,5
.
γ.
Δείξτε ότι η εξίσωση
( ) ( )
=
Ε x P x
είναι
αδύνατη.
δ.
Tο μέσο του ΑΔ.
ε.
Ο μαθητής έχει δίκιο.
Θέμα 60
Α. α.
Είναι
( )
( )
+ = +
f x
2e f x x 1
,
x
.
Θεωρείστε
( )
= +
t
π t 2e t
,
t
και
δείξτε ότι
π στο
1
.
β.
Είναι
( )
−
=
1
x f y
,
y
.
Β.
Θεωρείστε
( )
−
=
+
t
t
2e 1
κ t
e 7
,
t
και δείξ-
τε ότι
π στο
1
.
Γ.
(
)
− −
x 3, 1
Δ.
( )
= − − +
3
x
2
h x e x x 1
,
)
+
x 0,
.
Θέμα 61
α.
Προκύπτει ότι
+ = =
lnβ β 1 ...
β 1
.
β.
( )
−
−
−
=
3
1
x
, x 0
2
f x
x
, x 0
2
.









