351
Απαντήσεις -Υποδείξεις
= +
3
2
4
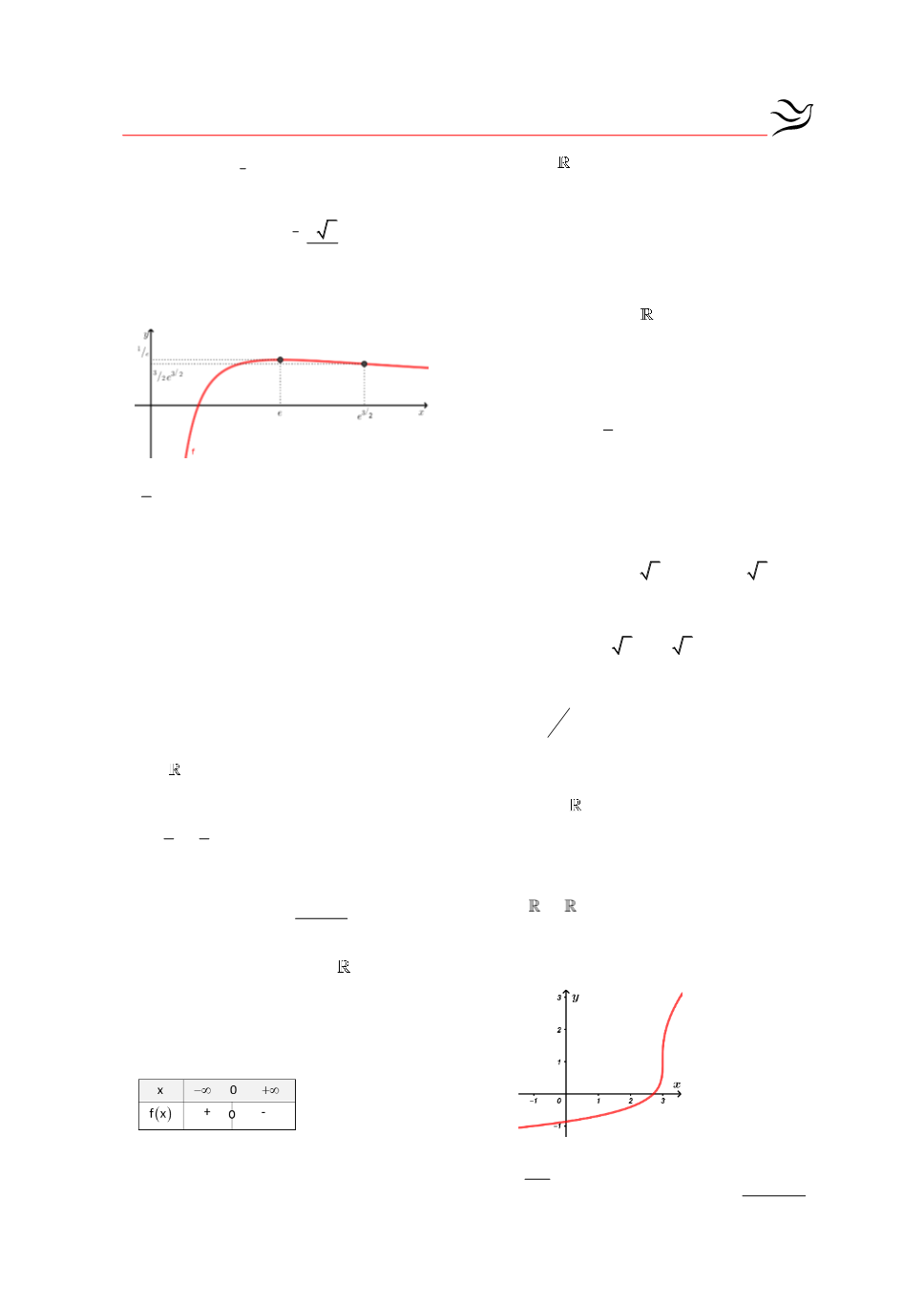
στο Δ e ,
3
Σημείο καμπής το
3
2
2
3 e
Α e ,
2e
γ.
Κατακόρυφη:
=
x 0
Οριζόντια:
=
y 0
στο
+
δ.
ε.
1
2
τ.μ.
Θέμα 21
α.
β 9 4α
= −
.
β.
α 2, β 1
= =
.
γ.
+
.
δ.
Θ.Ε.Τ. για την f στο
t 1,2
.
Θέμα 22
α.
Στο
1
−
συνεχής ως πηλίκο συνεχών
συναρτήσεων. Στο 1 βάση ορισμού.
β.
1 1
y x
2 2
= +
.
γ.
ming 0
=
.
Για
x 1
είναι
( )
( )
(
)
2
g x
f x
x 1
=
−
δ.
Είναι
( )
g x 0
για κάθε
x
με το «=»
μόνο για
x 1
=
.
Θέμα 23
α.
β.
Δεν υπάρχει.
γ.
1
f
D
−
=
.
δ.
Η εξίσωση είναι ισοδύναμη με την:
( )
f x 2016
=
.
ε.
Η αρχική σχέση ισοδύναμα γράφεται:
( )
(
)
(
)
f g x f lnx 2
= +
.
( )
1
x 2
g x e
−
−
=
,
x
.
Θέμα 24
α.
Είναι
( ) ( )( )
1
Ε x
ΟΑ ΟΒ
2
=
.
β.
(
1
στο Δ
, 2
= − −
1
,
)
2
στο Δ 2,0
= −
2
,
(
)
3
στο Δ 0,
= +
1
Τοπικό μέγιστο στο
1
x 2
= −
το
2
4e
−
γ.
(
στα
, 2 2
− − −
3
και
)
2 2,0
− +
και
(
)
0,
+
.
στα 2 2, 2 2
− − − +
4
.
δ.
(
)
e 2e 1 τ.μ.
−
.
ε.
μον 7
sec
.
Θέμα 25
α.
στο
1
.
(
στο
,1
−
4
,
)
στο 1,
+
3
.
Σημείο καμπής το
( )
Α 1,3
.
β.
( )
f
=
.
γ.
x 1
−
.
δ.
Στο
+
είναι η
( )
ε : y x
=
.
ε.
στ.
2
3e
2e τ.μ.
2
−









