Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
332
Θέμα 85
Β.
Να αποδείξετε ότι
( )
f x x
=
για κάθε
x
Î
.
Γ.
Δίνονται επιπλέον
●
η παραγωγίσιμη συνάρτηση
g :
®
με
( ) ( )
g x f x
³
για κάθε
x
Î
.
●
η παραγώγισιμη συνάρτηση
[
)
h: 0,
+¥ ®
με
( ) ( )
( )
g x
h x
f x
=
,
x 0
>
.
●
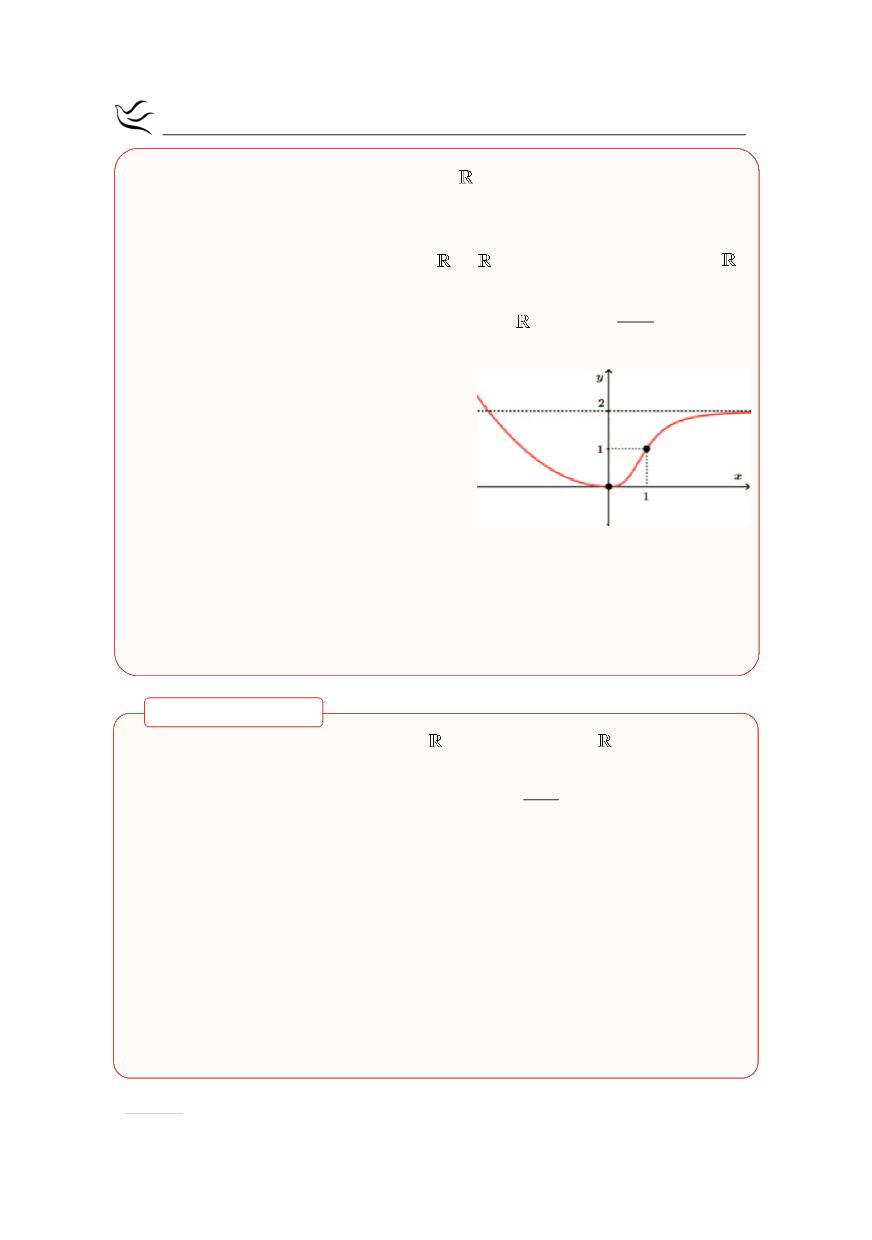
η γραφική παράσταση της παρα-
γώγου της συνάρτησης
g
όπως
φαίνεται στο διπλανό σχήμα
Γα
.
Να αποδείξετε ότι
( )
g 0 0
=
και
( )
x
lim g x
®+¥
= +¥
Γβ
.
Να αποδείξετε ότι η εφαπτομένη της
g
C
στο
( )
(
)
Α 1,g 1
είναι πάνω από
την εφαπτομένη της
h
C
στο
( )
(
)
Β 1,h 1
για κάθε
x 1
>
.
Γγ
.
Να βρείτε την ασύμπτωτη της
h
C
στο
+¥
.
Δίνονται οι συναρτήσεις
(
)
f : 1,
- +¥ ®
και
(
)
g : 1,
- +¥ ®
με
( ) (
)
f x ln x 1
= +
και
( )
x
g x
x 1
=
+
Α
.
Να λύσετε την εξίσωση
( ) ( )
f x g x 0
+ =
και να βρείτε το πρόσημο της συνάρ-
τησης
( ) ( ) ( )
Φ x f x g x
= +
.
Β
.
Να αποδείξετε ότι οι
f
C
και
g
C
δέχονται κοινή εφαπτομένη (ε) στο σημείο
( )
Ο 0,0
, η οποία διχοτομεί τη γωνία του πρώτου και τρίτου τεταρτημορίου.
Γ
.
Να υπολογίσετε το εμβαδόν του χωρίου Ω, που περικλείεται από τη
f
C
, την
(ε)
(από το ερώτημα
B)
και την ευθεία
ζ : x 3
=
.









