321
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Θέμα 68
Θέμα 69
β.
Να δείξετε ότι
( )
= +
2
f x x 1
,
Î
x
.
γ.
Να δείξετε ότι το σημείο της
f
C
που απέχει από το
( )
A 5,0
την μικρότερη
απόσταση είναι το
( )
M 1,2
.
δ.
Να βρείτε το εμβαδόν του χωρίου Ω που περικλείεται μεταξύ της
f
C
, του
άξονα
x
΄
x,
του άξονα
y
΄
y
και του ευθύγραμμου τμήματος ΑΜ
.
ε.
Να βρείτε την εξίσωση της ευθείας που διέρχεται από το Μ και χωρίζει το
χωρίο Ω, του ερωτήματος
δ
, σε δύο ισεμβαδικά χωρία.
Δίνεται η συνάρτηση
( )
(
)
= + + -
2
f x 13 x 144 5 40 x
,
³
x 0
.
Α
.
Να μελετήσετε την
f
ως προς τη μονοτονία και τα ακρότατα.
Β
.
Να βρείτε το σύνολο τιμών της
f
και το πρόσημό της.
Γ
.
Να αποδείξετε ότι η συνάρτηση
f
είναι κυρτή και ότι
( )
³ -
f x 356 5x
για κάθε
³
x 0
.
Δ
.
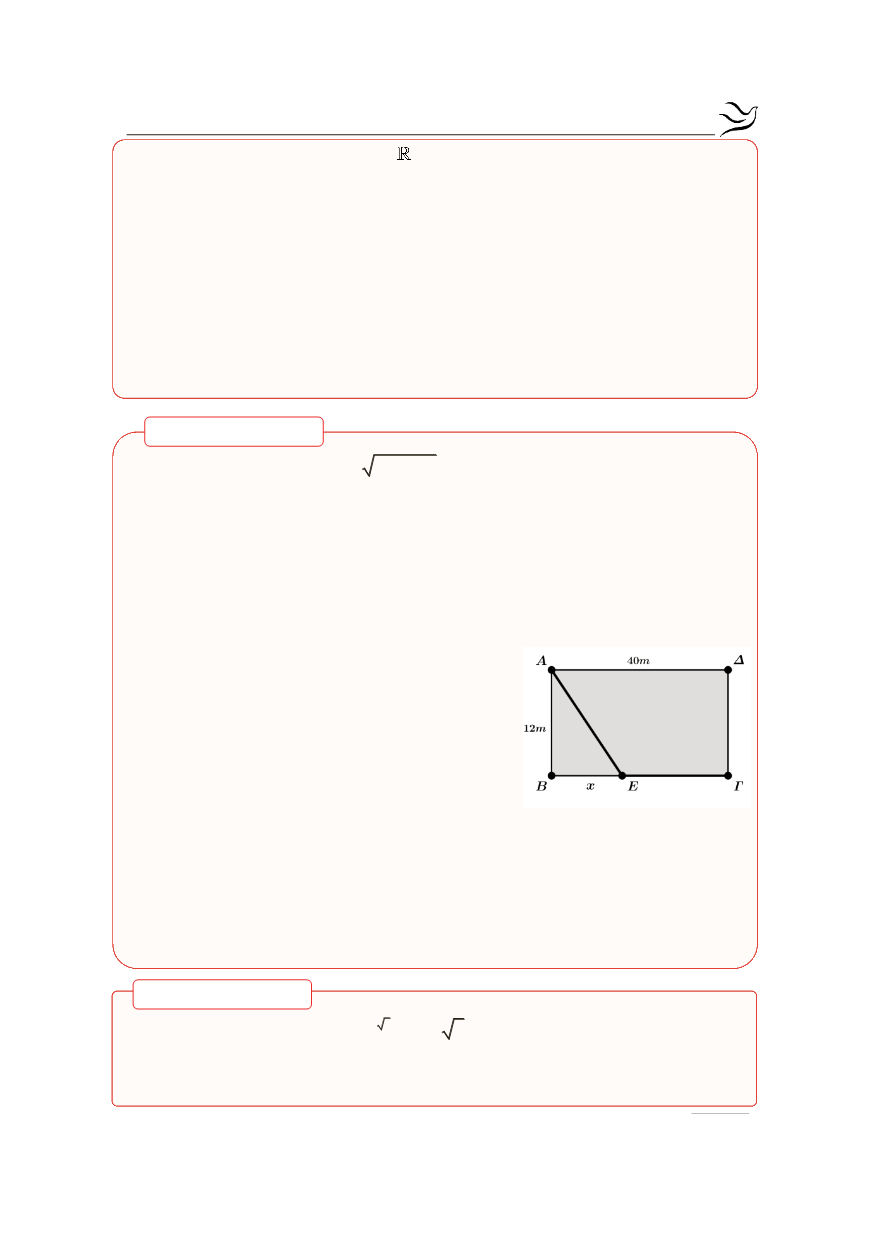
Ένας μηχανικός θέλει να χαράξει τη διαδρομή
ΑΕΓ στο ορθογώνιο οικόπεδο ΑΒΓΔ του σχή-
ματος για να περάσει από αυτή ένα καλώδιο
της ΔΕΗ. Η τοποθέτηση κοστίζει 13€/
m
για το
τμήμα ΑΕ του καλωδίου και 5€/
m
για το τμή-
μα ΕΓ.
α.
Να βρείτε τη συνάρτηση που εκφράζει το κόστος της τοποθέτησης του
καλωδίου για τη διαδρομή ΑΕΓ.
β.
Να βρείτε τη θέση του σημείου Ε, για την οποία το κόστος αυτής της το-
ποθέτησης είναι ελάχιστο καθώς και το ελάχιστο κόστος της εγκατάστα-
σης του καλωδίου κατά μήκος της διαδρομής ΑΕΓ.
Δίνεται η συνάρτηση
( )
(
)
= + -
x
f x ln e 1 x
με
³
x 0
.
α.
Να δείξετε ότι η
f
είναι γνησίως φθίνουσα.









