Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
316
Θέμα
59
Θέμα
60
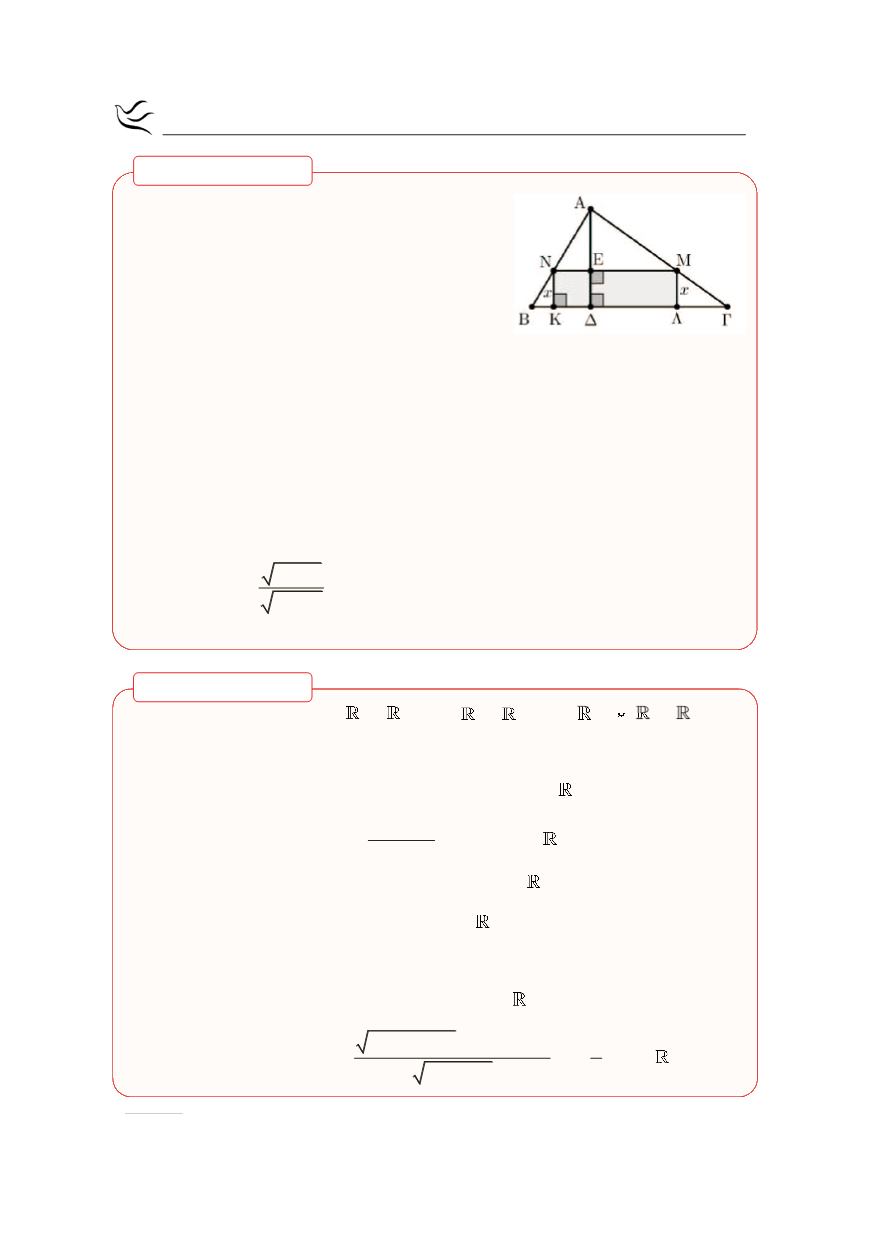
Ένα ορθογώνιο ΚΛΜΝ ύψους
x cm
είναι εγγε-
γραμμένο σε ένα τρίγωνο βάσης
( )
ΒΓ 10 cm
=
και ύψους
( )
ΑΔ 5 cm
=
.
α.
Να εκφράσετε το εμβαδόν Ε του ορθογωνί-
ου ως συνάρτηση του
x.
β.
Να εκφράσετε την περίμετρο
P
του ορθογωνίου ως συνάρτηση του
x.
γ.
Να δείξετε ότι δεν υπάρχει τιμή του
x
ώστε η αριθμητική τιμή του εμβαδού
του ορθογωνίου να είναι ίσο με την αριθμητική τιμή της περίμέτρου του.
δ.
Να βρείτε τη θέση του σημείου Ε ώστε το εμβαδόν του ορθογωνίου να γίνει
μέγιστο
.
ε.
Ένας μαθητής ισχυρίστηκε ότι το εμβαδόν του ΚΛΜΝ
μπορεί ναι γίνει
δύο
φορές ίσο με
7,777
4,444
. Να αναφέρετε αν συμφωνείται ή διαφωνείτε με τον
μαθητή αιτιολογώντας την απάντησή σας.
Δίν
o
νται οι
συναρτήσεις
®
f :
και
®
g :
με
( ) ( )
= =
f
g
για τις
οποίες ισχύουν:
( )
( )
- - = -
f x
2e x 1 f x
για κάθε
Î
x
( )
( )
( )
-
=
+
f x
f x
2e 7
g x
e 7
για κάθε
Î
x
Α. α.
Να δείξετε ότι η
f
είναι γνησίως αύξουσα στο
.
β.
Να δείξετε ότι
( )
-
= + -
1
x
f x 2e x 1
,
Î
x
και στη συνέχεια να βρείτε το
πρόσημο της
( )
f x
.
Β.
Να δείξετε ότι η
g
είναι γνησίως αύξουσα στο
Γ
.
Να λύσετε την ανίσωση
æ
ö
+ + + + +
< -
ç
÷
ç
÷
+ +
è
ø
3 2
2
3 2
2x 5x 4 x 4x 3 5
g
8
x x 1
στο
.









