309
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Θέμα
45
Θέμα
46
δ.
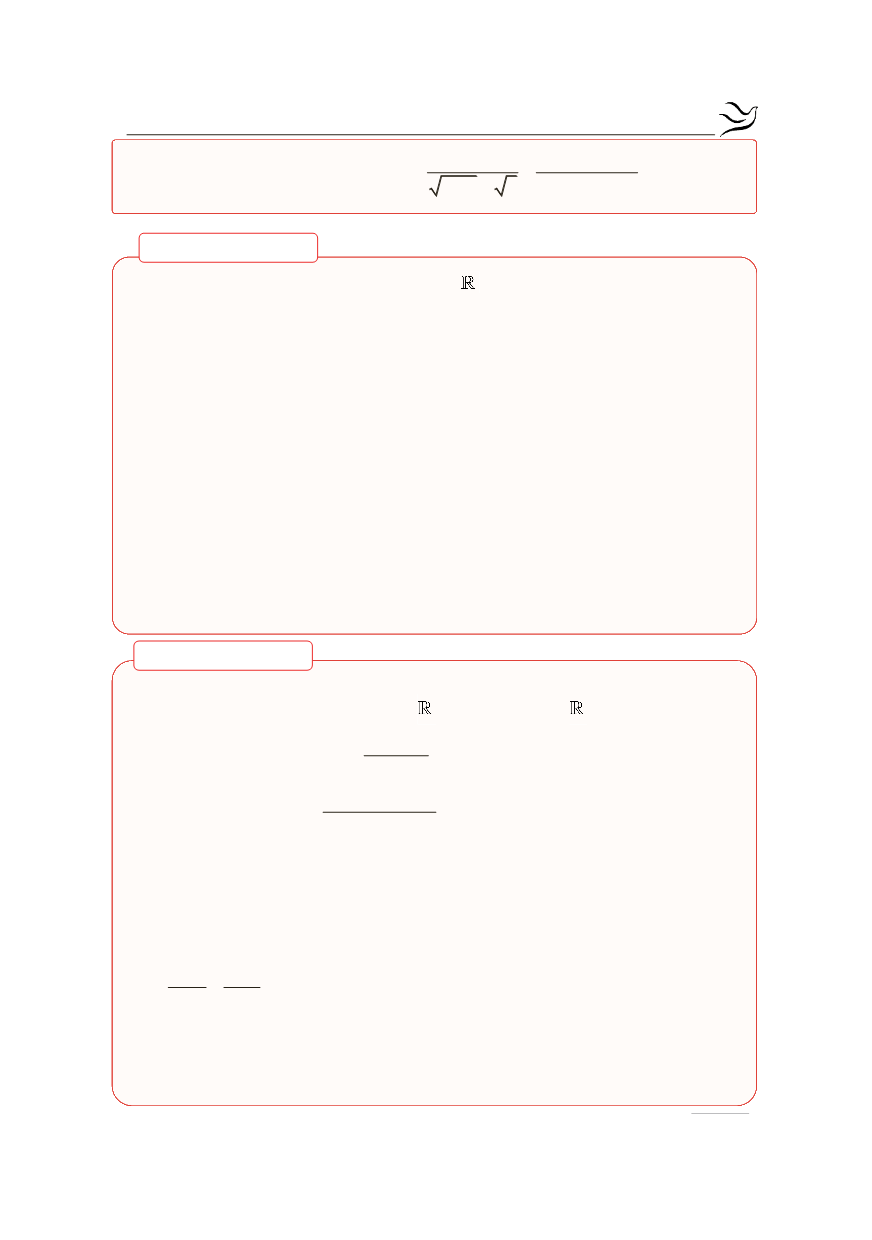
Να βρείτε, εφόσον υπάρχει,
το
( )
(
)
(
)
( )
x 1
ημ π x 1
g x
lim
g x
x 1 2
®
æ
ö -
+
ç
÷
ç
÷
+ -
è
ø
.
Δίνεται η συνάρτηση
( )
x
f x e x 2
= + -
,
Î
x
.
α.
Να δείξετε ότι η
f
είναι γνησίως αύξουσα και ότι υπάρχει μοναδικό
( )
α 0,1
Î
τέτοιο ώστε
α
e
α 2
+ =
.
β.
Να βρείτε το σύνολο τιμών της f και στη συνέχεια να βρείτε το πλήθος των
ριζών της εξίσωσης
( )
f x 2017
=
.
γ.
Να δείξετε ότι
> - + -
x
α
α
e xe
αe x α
για κάθε
>
x
α
.
δ.
Να δείξετε ότι η εξίσωση
(
)
(
)
( )
3f
α 2 2f α 1 5 f x x 3
¢
+ + + = é
+ - ù
ë
û
έχει μοναδική πραγματική λύση.
Δίνονται οι συναρτήσεις
(
)
+¥ ®
f : 1,
και
(
)
+¥ ®
g : 0,
με
( )
(
)
+
=
ln x 1
f x
lnx
και
( )
g x xlnx.
=
α.
Να δείξετε ότι
( ) ( ) (
)
(
)
- +
+
¢
=
2
g x g x 1
x
x x 1 ln
f
x
για κάθε
x 1
>
και να βρείτε τις ασύ-
μπτωτες της γραφικής παράστασης της
f.
β.
Να εξετάσετε την g ως προς τη μονοτονία, να βρείτε
το
(
)
(
)
+¥
g 1,
και να
λύσετε την εξίσωση
(
) ( )
3xln x 1 f x 0
+ + =
.
γ.
Αν
( ) ( )
+ £ -
g x g x
x 1
xln
α xlnβ
για κάθε
x 0
>
και
α,β 1
>
να δείξετε ότι
( )
ln
αβ lnαlnβ
=
.
δ.
Να δείξετε ότι
ln2018
ln2017
2018 2019
>
.









