293
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Θέμα 14
Θέμα 16
Θέμα 15
Δίνεται η συνάρτηση
( )
x
x
e
f x
, x
e 1
=
Î
+
.
α.
Να δείξετε ότι η
f
αντιστρέφεται.
β.
Να βρείτε
το πεδίο ορισμού και τον τύπο της
-
1
f
.
γ.
Να βρείτε
το κοινό σημείο
της γραφικής παράστασης της
-
1
f
με τον
x
΄
x.
δ
.
Να λύσετε
την εξίσωση
(
)
(
)
(
)
1
2f 3f f x 2 ln2 2 1
-
+ + - =
.
ε
.
Να υπολογίσετε, εφόσον υπάρχει, το
( )
3
1
3
x
x x
lim f
f x
2x ln3
-
®+¥
é
ù
æ
ö -
+
ê
ú
ç
÷ + è
ø
ë
û
Δίνονται οι συναρτήσεις
( )
f x 2 lnx
= -
,
x 0
>
και
( )
2x
2x
e
g x
3 e
=
+
,
x
Î
.
α.
Να δείξετε ότι η
g
αντιστρέφεται
και
να βρείτε
τον τύπο της
1
g
-
.
β.
Να βρείτε το πεδίο ορισμού και τον τύπο της συνάρτησης
1
f g
-
.
γ.
Να λύσετε την ανίσωση
( )
(
)
1
ln3
g f x
2
-
>
δ.
Να υπολογίσετε το
(
)
( )
1
x 1
lim f g x
-
-
®
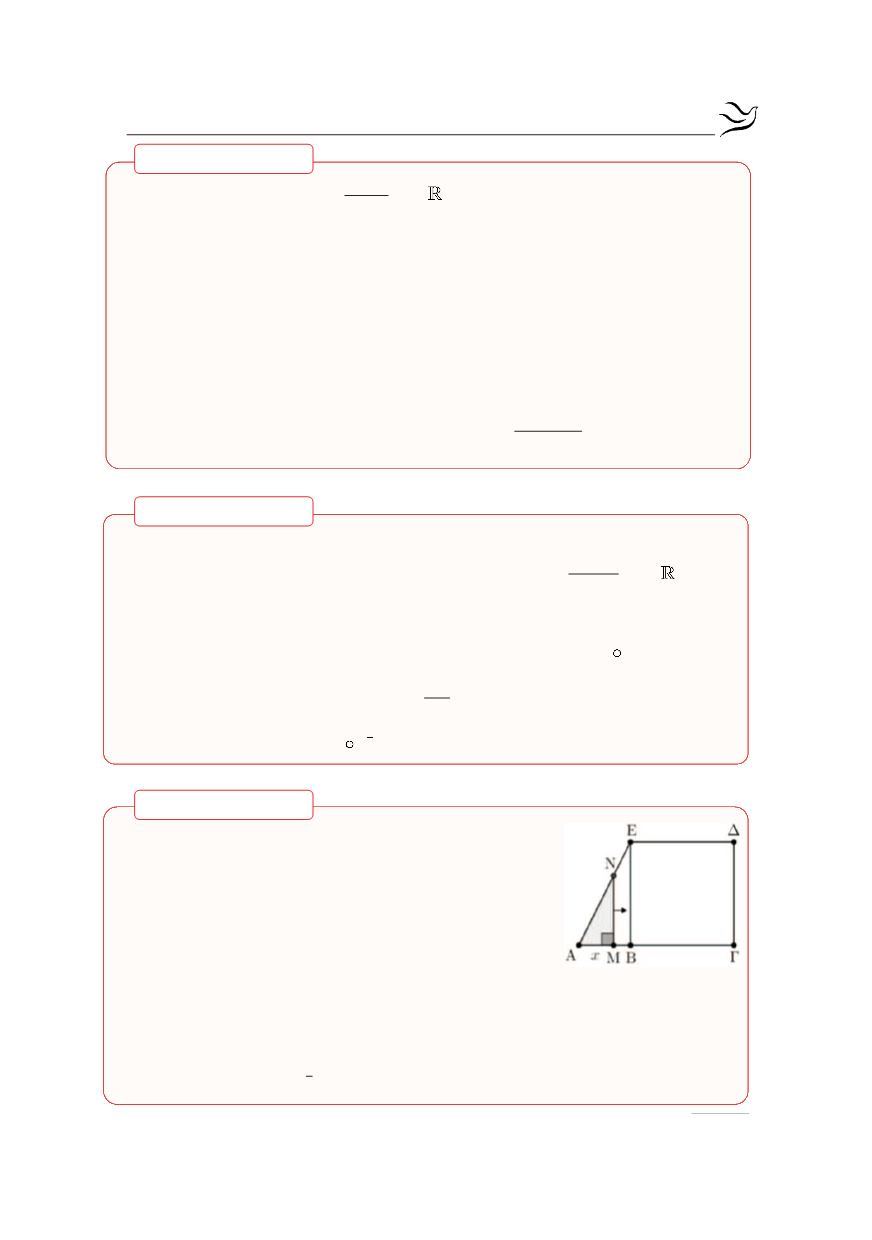
Στο διπλανό σχήμα είναι
( )
ΑΒ 1
=
,
( )
ΑΓ 3
=
,
( )
ΓΔ 2
=
και Μ τυχαίο σημείο της ΑΓ ώστε
( )
ΑΜ x
=
,
0 x 3
< £
.
α.
Να εκφράσετε το εμβαδόν
( )
Ε x
του γραμμοσκια-
σμένου χωρίου ως συνάρτηση του
x.
β.
Να εξετάσετε αν η
( )
Ε x
είναι συνεχής και παραγωγίσιμη
.
γ.
Να δείξετε ότι η
( )
Ε x
αντιστρέφεται και να βρείτε την
( )
1
Ε x
-
.
δ.
Να υπολογίσετε το
( )
2
1
2
Ε x dx
ò
.









