237
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
( )
(
)
3
3 3
2
2
x
x
x
x
x x x
lim f x x lim x lim
x 1
x 1
®+¥
®+¥
®+¥
æ
ö
- -
- =
- =
ç
÷
+
+
è
ø
2
2
x
x
x
x
x
1
lim lim lim 0
x 1
x
x
®+¥
®+¥
®+¥
-
-
-
=
=
=
=
+
Άρα
( )
1
ε : y x
=
πλάγια ασύμπτωτη της γραφικής παράστασης της
f
στο
+¥
.
( )
3
3
3
2
3
3
x
x
x
x
x
f x
x
x
x 1
lim lim lim lim 1
x
x
x x
x
®-¥
®-¥
®-¥
®-¥
+
=
=
=
=
+
( )
(
)
3
3 3
2
2
x
x
x
x
x x x
lim f x x lim x lim
x 1
x 1
®-¥
®-¥
®-¥
æ
ö
- -
- =
- =
ç
÷
+
+
è
ø
2
2
x
x
x
x
x
1
lim lim lim 0
x 1
x
x
®-¥
®-¥
®-¥
-
-
-
=
=
=
=
+
Άρα
( )
1
ε : y x
=
πλάγια ασύμπτωτη της γραφικής παράστασης της
f
στο
-¥
.
Γ3.
Έχουμε:
(
)
(
)
(
)
(
)
(
)
(
)
f
3
2
3
2
2
2
2
2
f 5 x 1 8 f 8 x 1 5 x 1 8 8 x 1
+ - £
+ Û + - £ +
1
(1)
Έστω
2
θ x 1
= +
με
θ 1
³
.
Οπότε η
(1)
γίνεται:
3
2
3
2
5
θ 8 8θ 5θ 8θ 8 0
- £ Û - - £
(2)
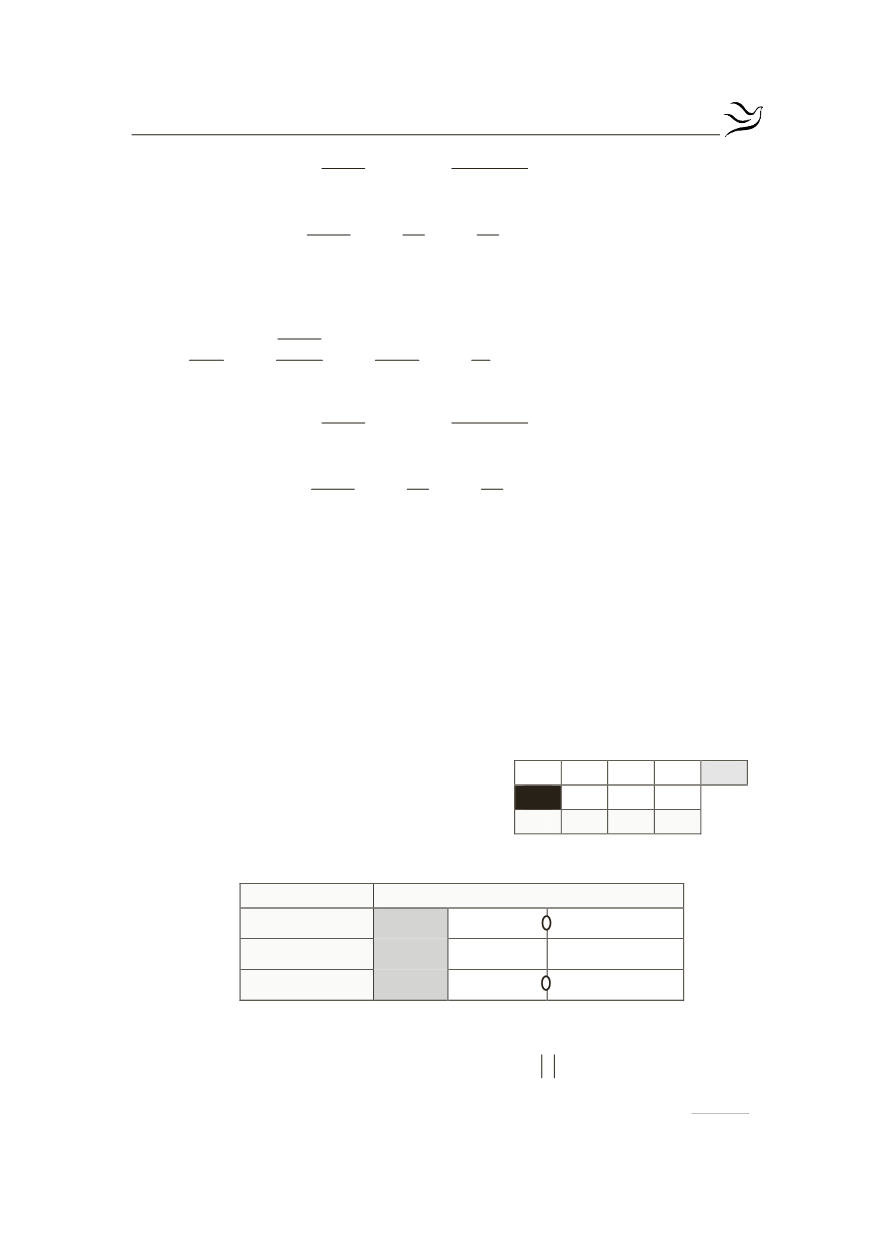
Από το διπλανό σχήμα
Horner
έχουμε:
Η
(2)
γίνεται:
(
)
(
)
2
θ 2 5θ 2θ 4 0
-
+ + £
·
θ 2 0 θ 2
- = Û =
·
2
5
θ 2θ 4 0
+ + =
,
Δ 4 80 76 0
= - = - <
Από τον παραπάνω πίνακα προσήμου έχουμε :
2
2
1
θ 2 1 x 1 2 0 x 1 x 1 1 x 1
£ £ Û £ + £ Û £ £ Û £ Û- £ £
θ
-¥
1 2
+¥
θ 2
-
-
+
2
5
θ 2θ 4
+ +
+
+
Γινόμενο
-
+
5
-8
0
-8
2
10
4
8
5
2
4
0









