233
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Γ2.
Η συνάρτηση f είναι παραγωγίσιμη στο
με
( )
2
f ' x
=
x
2
2
2
2
x x 1
1
x 1
x 1
- +
- =
+
+
Το πρόσημο και οι ρίζες της f ’ εξαρτώνται από την
( )
2
φ x x x 1
= - +
, με
φ
D
=
·
Για
x 0
>
είναι
2
2
2 2
x x 1 0 x x 1 x x 1 1 0
- + < Û < + Û < + Û >
, που
ισχύει
·
Για
x 0
<
είναι
2
2
x x 1 0 x 1 x
- + < Û + >
, που
ισχύει
·
Για
x 0
=
είναι
1 0
- <
, που ισχύει
.
Άρα
( )
f ' x 0
<
για κάθε
x
Î
οπότε
η f είναι γνησίως φθίνουσα στο
R
.
Ε-
πομένως
είναι "1
-1".
Έχουμε διαδοχικά:
( )
(
)
( )
(
)
( )
( )
2
f "1 1"
3
3x
f g x 1 f g x f 0
g x 0 x
1 0
2
-
= Û =
Û = Û + - =
Η g είναι παραγωγίσιμη στο
με
( )
(
)
2
g' x 3x 3x 3x x 1
= + = +
, με
x
Î
.
·
g
γνησίως αύξουσα στο
(
]
1
Δ
, 1
= -¥ -
και συνεχής άρα
( )
( ) ( )
(
1
x
g
Δ lim g x ,g 1
®-¥
ù
=
-
û
Όμως
( )
( )
2
3
3
x
x
x
3x
lim g x lim x
1 lim x
2
®-¥
®-¥
®-¥
æ
ö
=
+ - =
= -¥
ç
÷
è
ø
Οπότε
( )
1
1
g
Δ
,
2
æ
ù
= -¥ - ç
ú
è
û
.
Παρατηρούμε ότι
( )
1
0 g
Δ
Ï
.
·
g
γνησίως φθίνουσα στο
[
]
2
Δ 1,0
= -
και συνεχής, άρα
( )
( ) ( )
2
1
g
Δ g 0 ,g 1
1,
2
é
ù
= é
- ù = - -
ë
û ê
ú
ë
û
. Παρατηρούμε ότι
( )
2
0 g
Δ
Ï
.
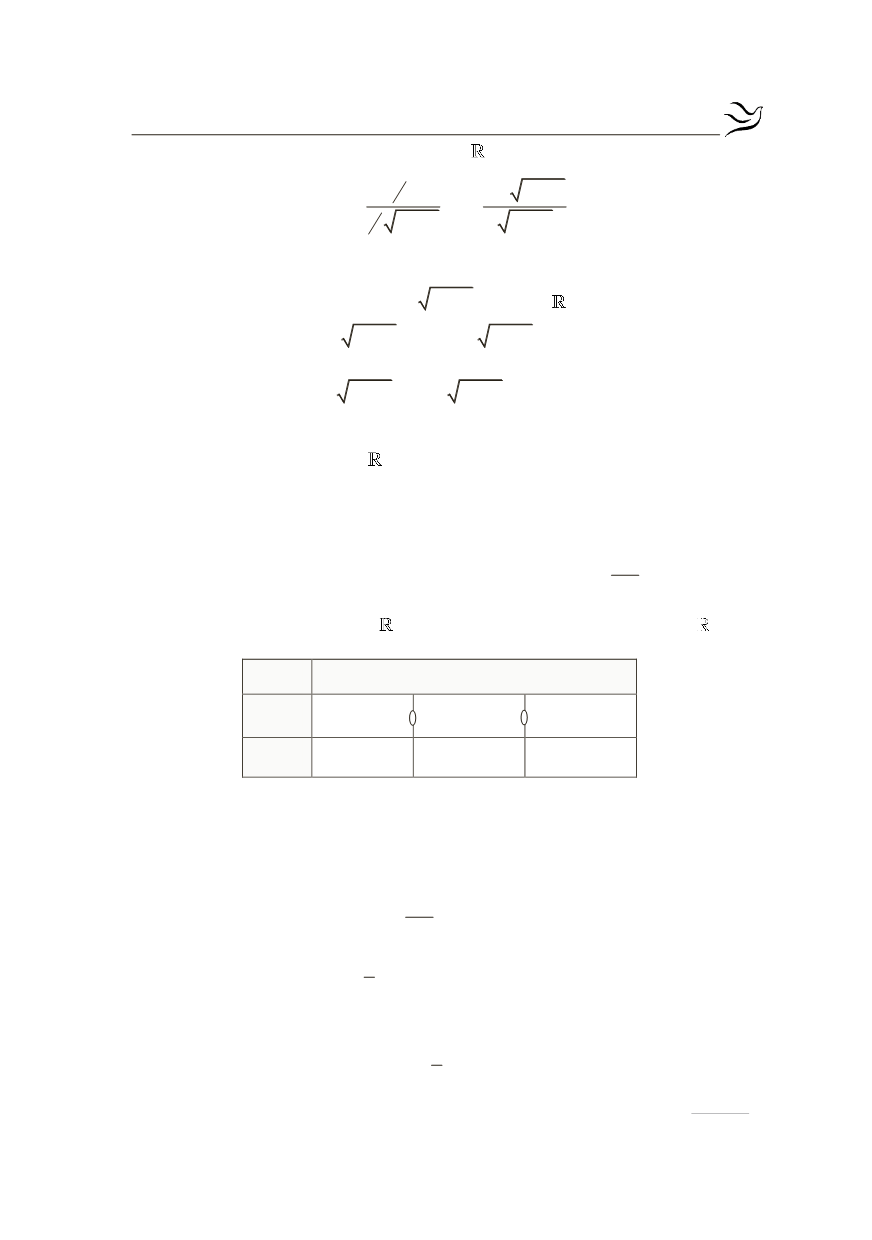
x
-
¥
-1 0
+
¥
( )
g x
¢
+
-
+
g
1
>
1









