Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
228
( ) ( )
0
0
f x f x 2012
¢Û + =
και αποδείχθηκε το ζητούμενο
Γ4.
Είναι:
( ) ( )
(
)
(
)
g x f x 1 x 1 lnx 1 1 x 1 lnx
= + = - - + = -
,
(
)
x 0,
Î +¥
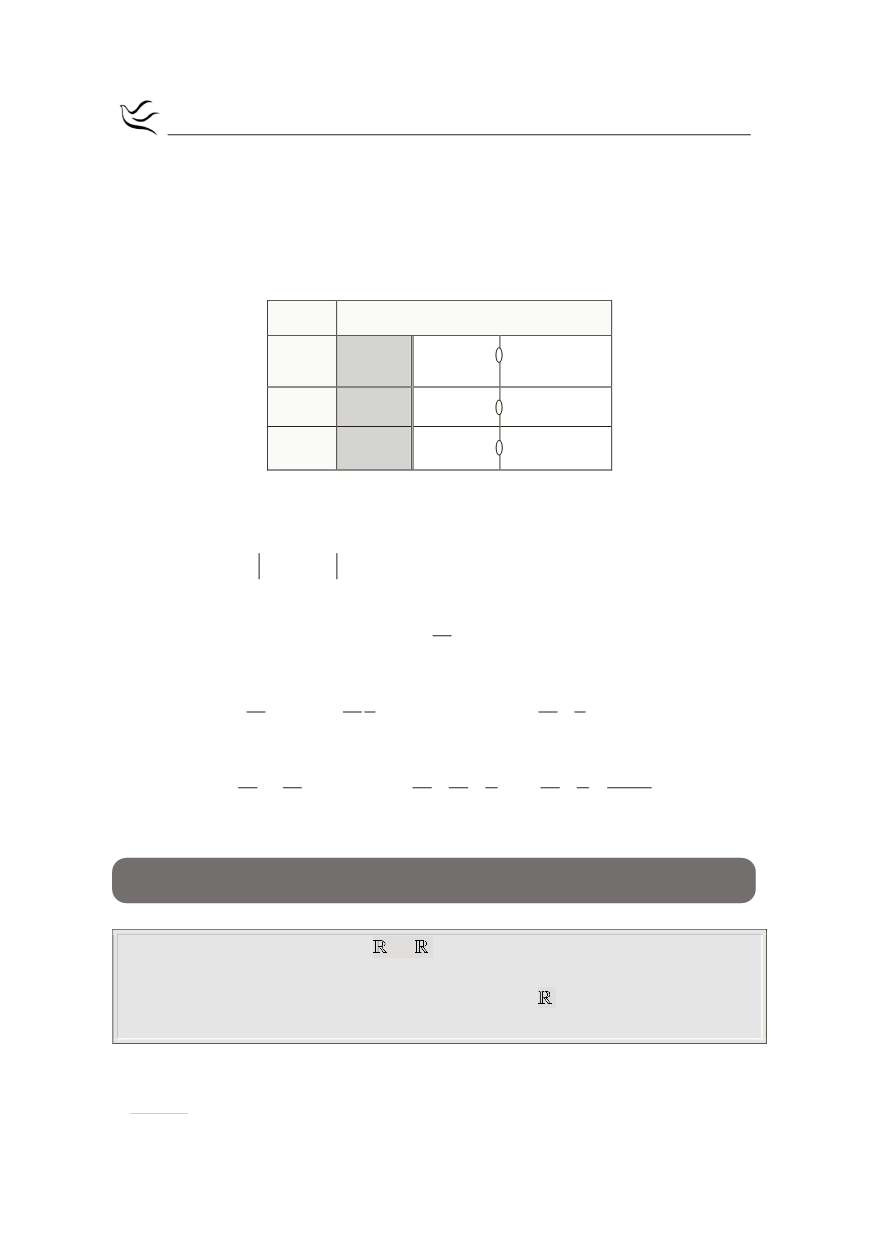
Το πρόσημο της φαίνεται στον παρακάτω πίνακα:
Άρα:
(
)
(
)
e
e
1
1
Ε(Ω)
x 1 lnx dx
x 1 lnxdx
= -
= -
=
ò
ò
( )
2
e
e
e
e
1
1
1
1
x
xlnxdx lnxdx
lnxdx x lnxdx
2
¢
æ ö
¢
=
-
=
-
=
ç ÷
è ø
ò
ò
ò
ò
[
]
[ ]
e
2
2
2
e
e
e
e
e
1
1
1
1
1
1
x
x 1
e 1
lnx
dx xlnx
dx
xdx e x
2
2 x
2 2
é
ù
=
-
-
+ = -
- + =
ê
ú
ë
û
ò
ò
ò
e
2
2
2
2
2
2
1
e x
e e 1 e 3 e 3
e e 1
1
τ.μ.
2 4
2 4 4 4 4 4
é ù
-
= - - + - = - + - = - =
ê ú
ë û
Έστω η συνεχής συνάρτηση
f :
®
, για την οποία ισχύει:
( )
x
xf x 1 e
+ =
, για κάθε
x
Î
x
-
¥
0 1
+
¥
x 1
-
-
+
lnx
-
+
( )
g x
+
+
ΘΕΜΑ Γ
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2012









