Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
226
Ακόμη, είναι:
·
( )
( ) ( )
f
f x 0 f x f 1 0 x 1
¢
¢
¢
< Û < Û < <
1
.
·
( )
( ) ( )
f
f x 0 f x f 1 x 1
¢
¢
¢
> Û > Û >
1
.
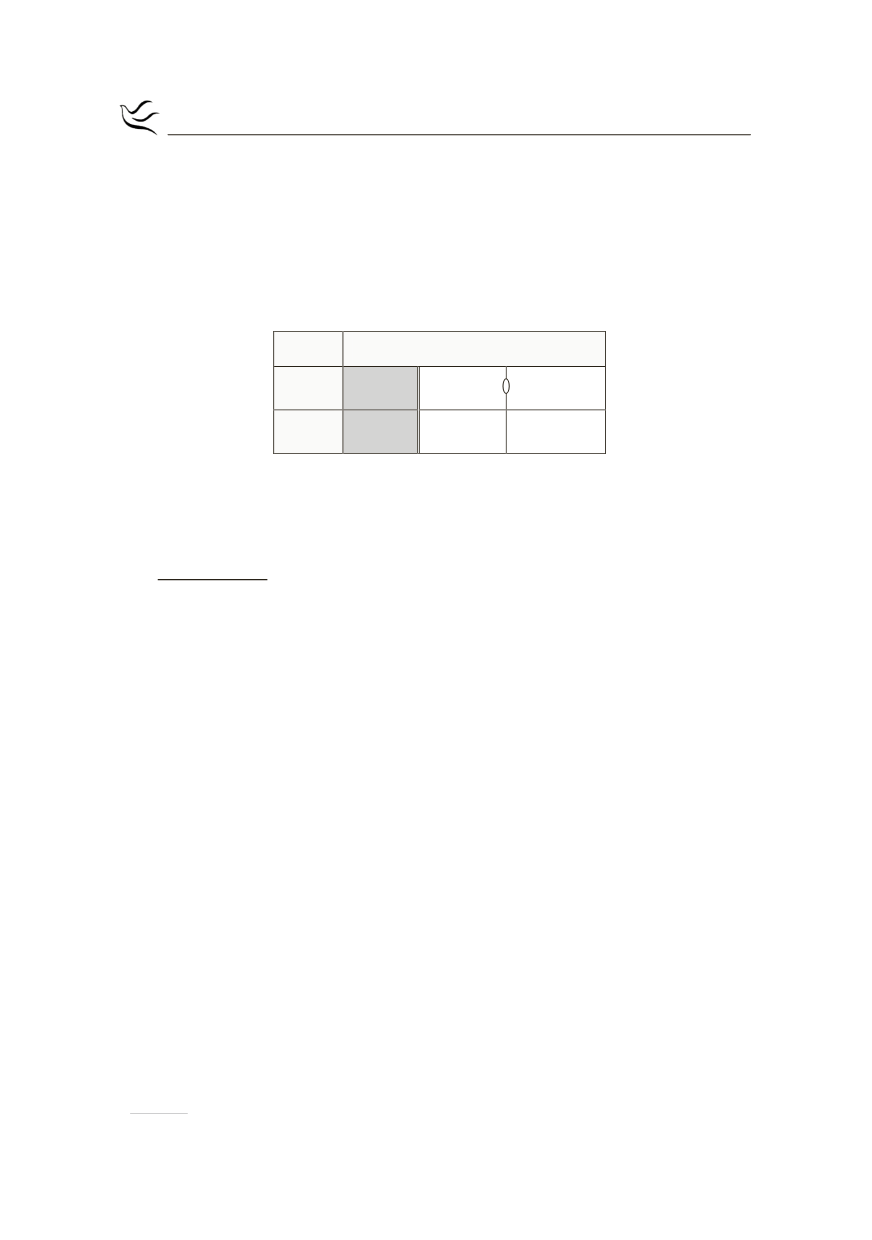
Συνοπτικά, το πρόσημο της
f
¢
καθώς και η μονοτονία της
f
φαίνονται στον
παρακάτω πίνακα:
·
Η
f
είναι γνησίως φθίνουσα στο
(
]
0,1
·
Η
f
είναι γνησίως αύξουσα στο
[
)
1,
+¥
Σύνολο τιμών
Ø
Η
f
συνεχής και γνησίως φθίνουσα στο
(
]
1
Δ 0,1
=
επομένως
( )
( )
)
1
x 0
f
Δ f 1 , lim f(x)
+
®
é= êë
Όμως,
[
]
x 0
x 0
lim f(x) lim (x 1)lnx 1
+
+
®
®
=
- - = +¥
και
( ) (
)
f 1 1 1 ln1 1 0 1 1
= - - = - = -
άρα
( )
[
)
1
f
Δ 1,
= - +¥
Ø
Η
f
συνεχής και γνησίως αύξουσα στο
[
)
2
Δ 1,
= +¥
επομένως
( )
( )
)
2
x
f
Δ f 1 , lim f(x)
®+¥
é=
ë
Όμως ,
[
]
x
x
lim f(x) lim (x 1)lnx 1
®+¥
®+¥
=
- - = +¥
άρα
( )
[
)
2
f
Δ 1,
= - +¥
Τελικά, το σύνολο τιμών της
f
είναι:
( ) ( ) ( )
[
)
[
)
[
)
f
1
2
f D f
Δ f Δ 1,
1,
1,
= È = - +¥ È - +¥ = - +¥
Γ2.
Η εξίσωση γίνεται:
( ) (
)
lnx''1 1''
x 1 2013
x 1
2013
x e
ln x
ln e
-
-
-
= Û =
(
)
(
)
x 1 lnx 2013 x 1 lnx 1 2012
Û - = Û - - =
x
-
¥
0 1
+
¥
( )
f x
¢
-
+
( )
f x
>
1









