Μαθηματικά Γ' Λυκείου

222 / 368

221
Μαθηματικά Προσανατολισμού – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Έστω 1 2
π
x ,x 0,
2
é ù
Î ê ú ë ûμε 1 2 x x< τότε
( ) ( )
1 2 1 2 x x f x f x< Û < (1) διότι f 1 στο [0, ) +¥
1 2 1 2 1 2 x x συνx συνx συνx συνx < Û > Û - < - (2) διότι συνx 2 στο
π
0,
2
é ù
ê ú ë û
Έτσι με πρόσθεση κατά μέλη των (1) και (2) έχουμε :
( ) ( )
1 1 2 2 f x συνx f x συνx - < - , άρα ( ) ( )1 2 g x g x<
Επομένως g γνησίως αύξουσα στο
π
0,
2
é ù
ê ú ë û άρα και 1-1 δηλαδή η ρίζα εί-
ναι μοναδική.
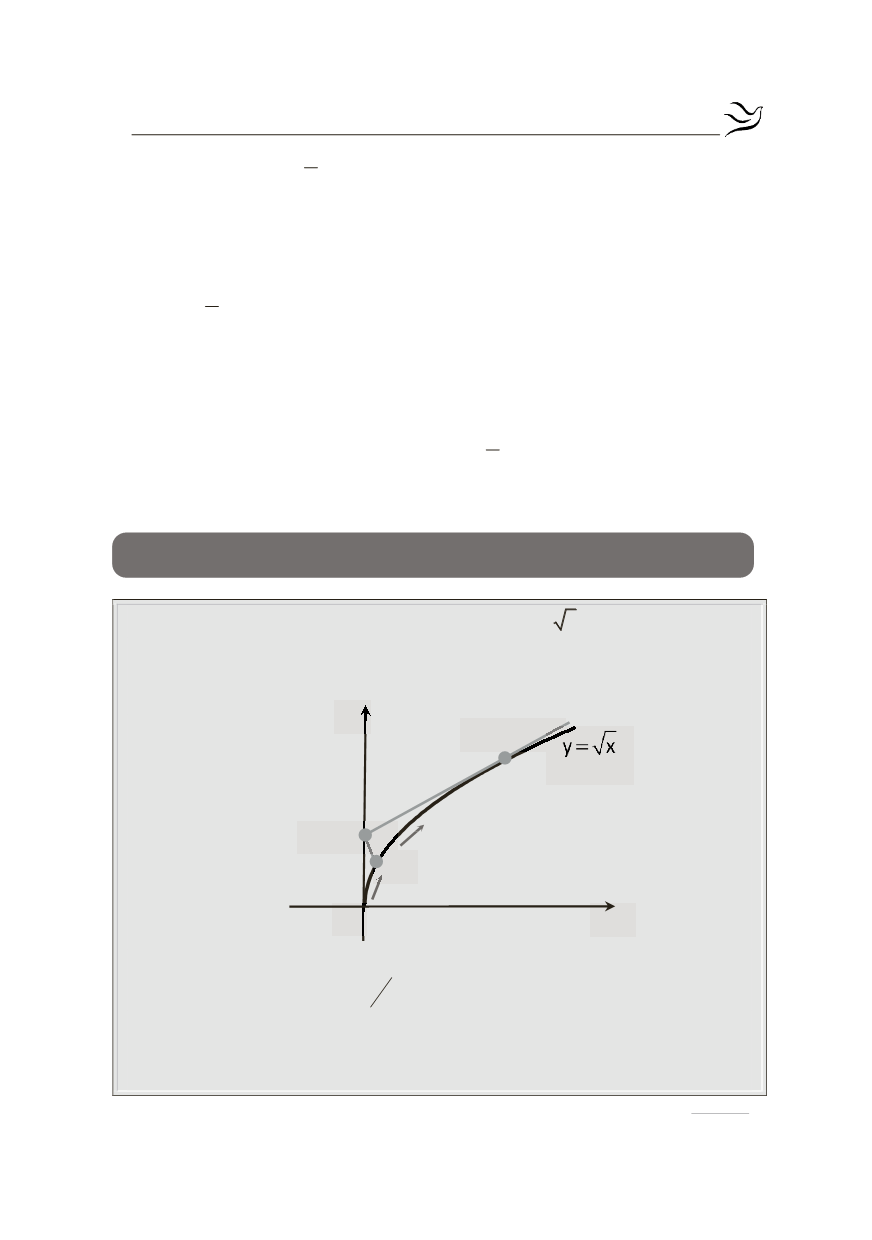
Ένα κινητό Μ κινείται κατά μήκος της καμπύλης y x= , x 0³ . Ένας παρατη-
ρητής βρίσκεται στη θέση Π(0,1) ενός συστήματος συντεταγμένων Οxy και πα-
ρατηρεί το κινητό από την αρχή Ο, όπως φαίνεται στο παρακάτω σχήμα.
Δίνεται ότι ο ρυθμός μεταβολής της τετμημένης του κινητού για κάθε χρονική
στιγμή t, t 0³ είναι ( ) m x t 16
min
¢ =
Γ1. Να αποδείξετε ότι η τετμημένη του κινητού, για κάθε χρονική στιγμή t,
t 0³ δίνεται από τον τύπο ( )
x t 16t= .
(Μονάδες 5)
ΘΕΜΑ Γ ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2011
x
y
Ο
Π(0,1)
Α(4,2)
Μ