Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
218
Οι ρίζες και το πρόσημο της
( )
f
΄ x
εξαρτώνται μόνο από τις ρίζες και το
πρόσημο του αριθμητή αφού
( )
h x 0
>
για κάθε
x
Î
, όπως δείξαμε στο
Γ1
Συνεπώς ,
( )
( )
f x 0 h x 0 x 0
¢
¢
= Û = Û =
( )
( )
f
΄ x 0 h x 0 x 0
¢
> Û > Û >
( )
( )
f
΄ x 0 h΄ x 0 x 0
< Û < Û <
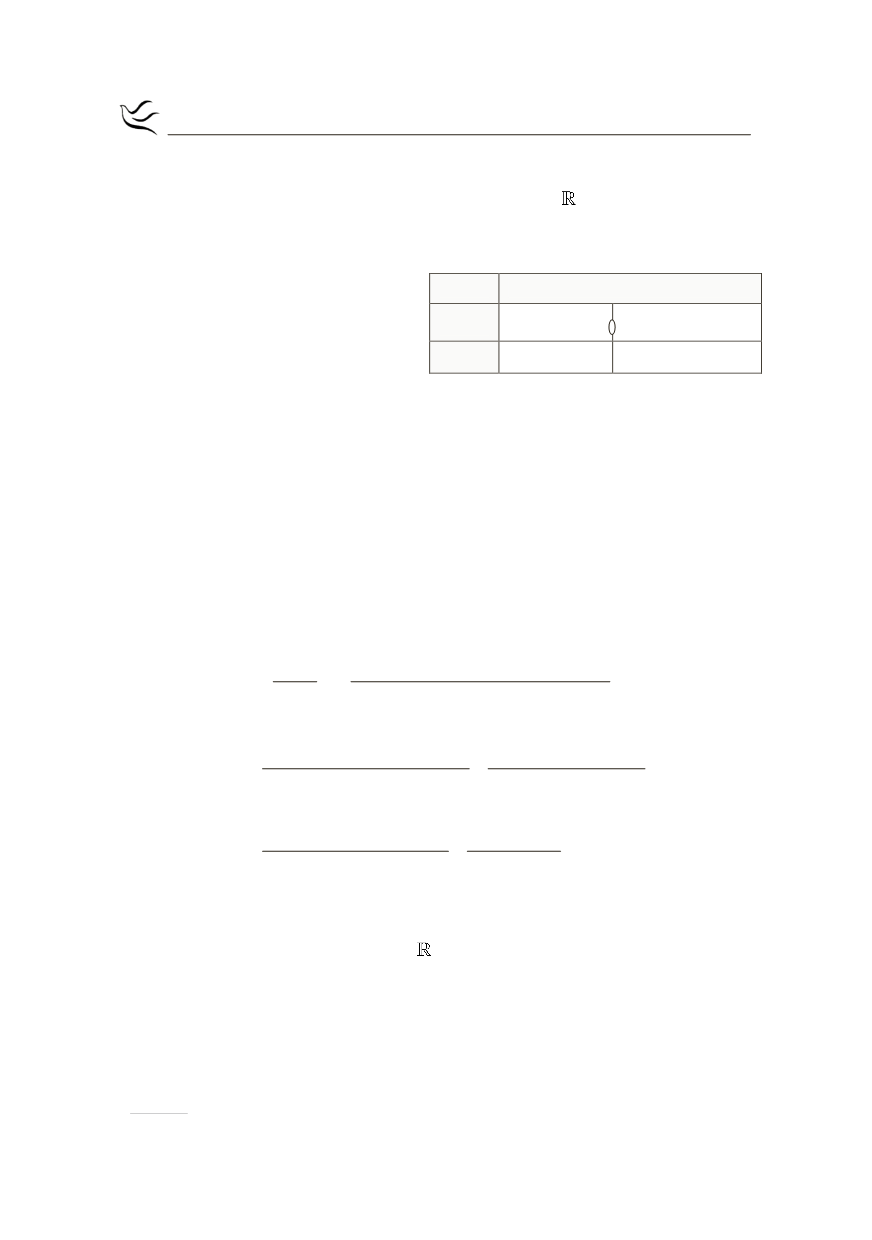
Από τον παραπάνω πίνακα μεταβολών
·
H f
είναι γνησίως φθίνουσα στο
(
]
,0
-¥
·
H f
είναι γνησίως αύξουσα στο
[
)
0,
+¥
·
Η
f
παρουσιάζει ολικό ελάχιστο στη θέση
x 0
=
με τιμή
( )
(
)
0
f 0 ln e 0 ln1 0.
= - = =
Γ3.
Είναι:
( )
(
) (
) (
)(
)
(
)
x
x
x
x
x
2
x
x
e 1 e x e 1 e x
e 1
f x
e x
e x
¢
¢
¢
- - - - -
æ
ö-
¢
=
=
ç
÷ - è
ø
-
(
) (
)(
)
(
)
(
) (
)
(
)
2
x x
x
x
x x
x
2
2
x
x
e e x e 1 e 1 e e x e 1
e x
e x
- - - -
- - -
=
=
-
-
(
)
(
)
(
)
(
)
2x
x
2x
x
x
2
2
x
x
e xe e 2e 1 2 x e 1
e x
e x
- - - +
- -
=
=
-
-
Οι ρίζες και το πρόσημο της
f
¢¢
εξαρτώνται μόνο από τον αριθμητή
Θέτουμε
( ) (
)
x
φ x 2 x e 1,
= - -
x
Î
.
Είναι:
( ) (
)
(
)
( )
(
)
(
)
x
x
x
x
x
φ x 2 x e 2 x e e 2 x e e 1 x
¢
¢
¢
= - + -
= - + - = -
·
( )
(
)
x
φ x 0 e 1 x 0 1 x 0 x 1
¢
= Û - = Û - = Û =
x
-
¥
0
+
¥
( )
f x
¢
-
+
f
>
1









