Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
206
Επιπλέον :
·
( )
( ) ( )
f
f x 0 f x f 0 x 0
¢
¢
¢
¢
> Û > Û >
1
·
( )
( ) ( )
f
f x 0 f x f 0
1 x 0
¢
¢
¢
¢
< Û < Û - < <
1
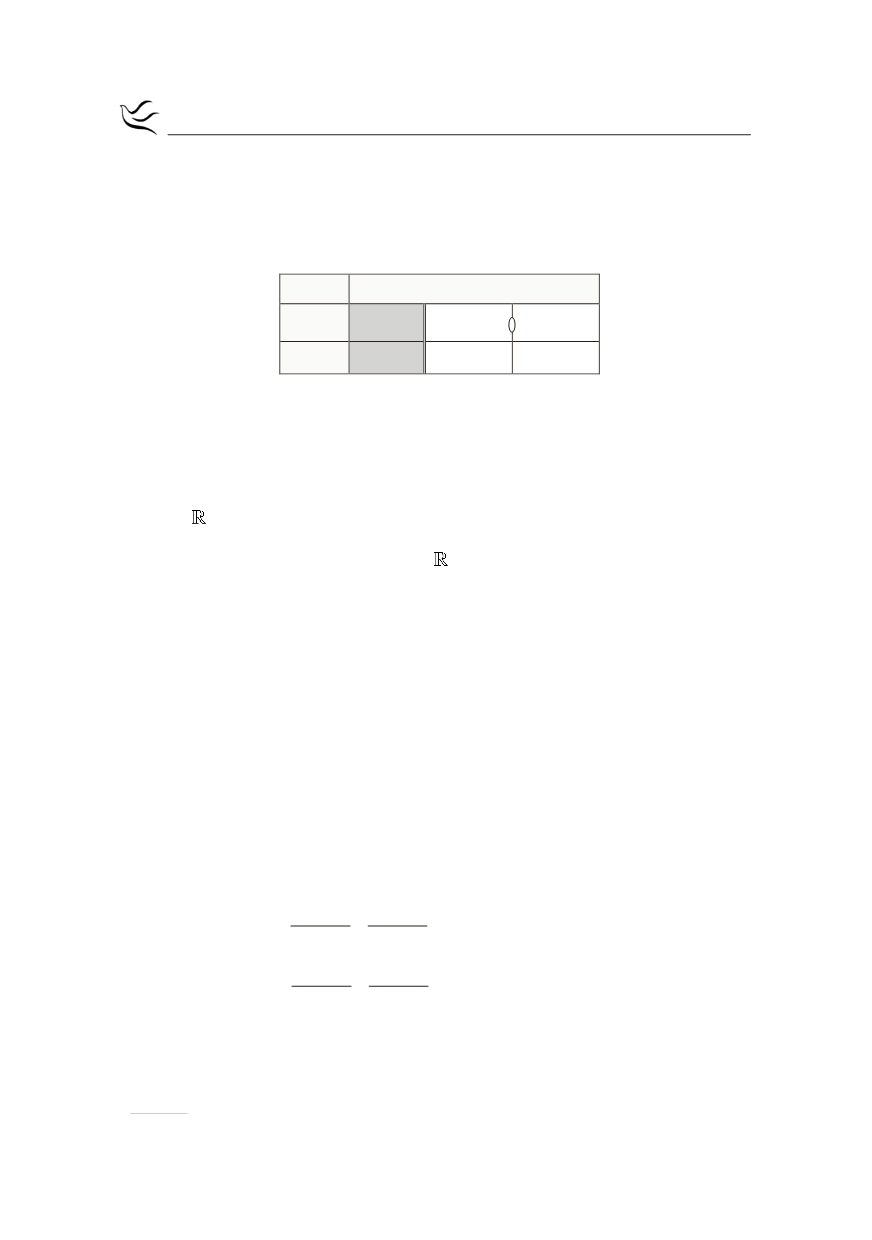
Από τον παραπάνω πίνακα μεταβολών έχουμε ότι η
f
είναι γνησίως φθί-
νουσα στο
(
]
1,0
-
και γνησίως αύξουσα
στο
[
)
0,
+¥
.
γ.
Θεωρούμε τη συνάρτηση
( )
( )
(
)
(
) ( )
(
)
(
)
g x f
β 1 x 2 f γ 1 x 1
= - - + - -
με
g
D
=
·
H g είναι συνεχής στο
[ ]
1,2
Í
ως πολυωνυμική
·
( )
( )
(
)
(
) ( )
(
)
(
)
( )
g 1 f
β 1 1 2 f γ 1 1 1 1 f β 0
= - - + - - = - <
αφού η
f
πα-
ρουσιάζει ολικό ελάχιστο μόνο στο
0 άρα
( ) ( )
f
β f 0
³
και
β 0
¹
άρα
( ) ( )
( )
( )
f
β f 0 f β 1 1 f β 0
> Û > Û - <
( )
( )
(
)
(
) ( )
(
)
(
) ( )
g 2 f
β 1 2 2 f γ 1 2 1 f γ 1 0
= - - + - - = - >
αφού
( ) ( )
f
γ f 0
³
και
γ 0
¹
άρα
( ) ( )
( )
( )
f
γ f 0 f γ 1 f γ 1 0
> Û > Û - >
Άρα,
( ) ( )
g 1 g 2 0
×
<
, οπότε σύμφωνα με το θεώρημα Bolzano υπάρχει
τουλάχιστον ένα
( )
0
x 1,2
Î
τέτοιο, ώστε
( )
0
g x 0
= Û
( )
(
)
(
) ( )
(
)
(
)
0
0
f
β 1 x 2 f γ 1 x 1 0
- - + - - =
( )
( )
0
0
f
β 1 f γ 1
0
x 1 x 2
-
-
Û +
=
-
-
Άρα η εξίσωση
( )
( )
f
β 1 f γ 1
0
x 1 x 2
-
-
+
=
-
-
έχει τουλάχιστον μια ρίζα στο
( )
1,2
.
x
-
¥
-1 0
+
¥
( )
f x
¢
-
+
f
>
1









