Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
200
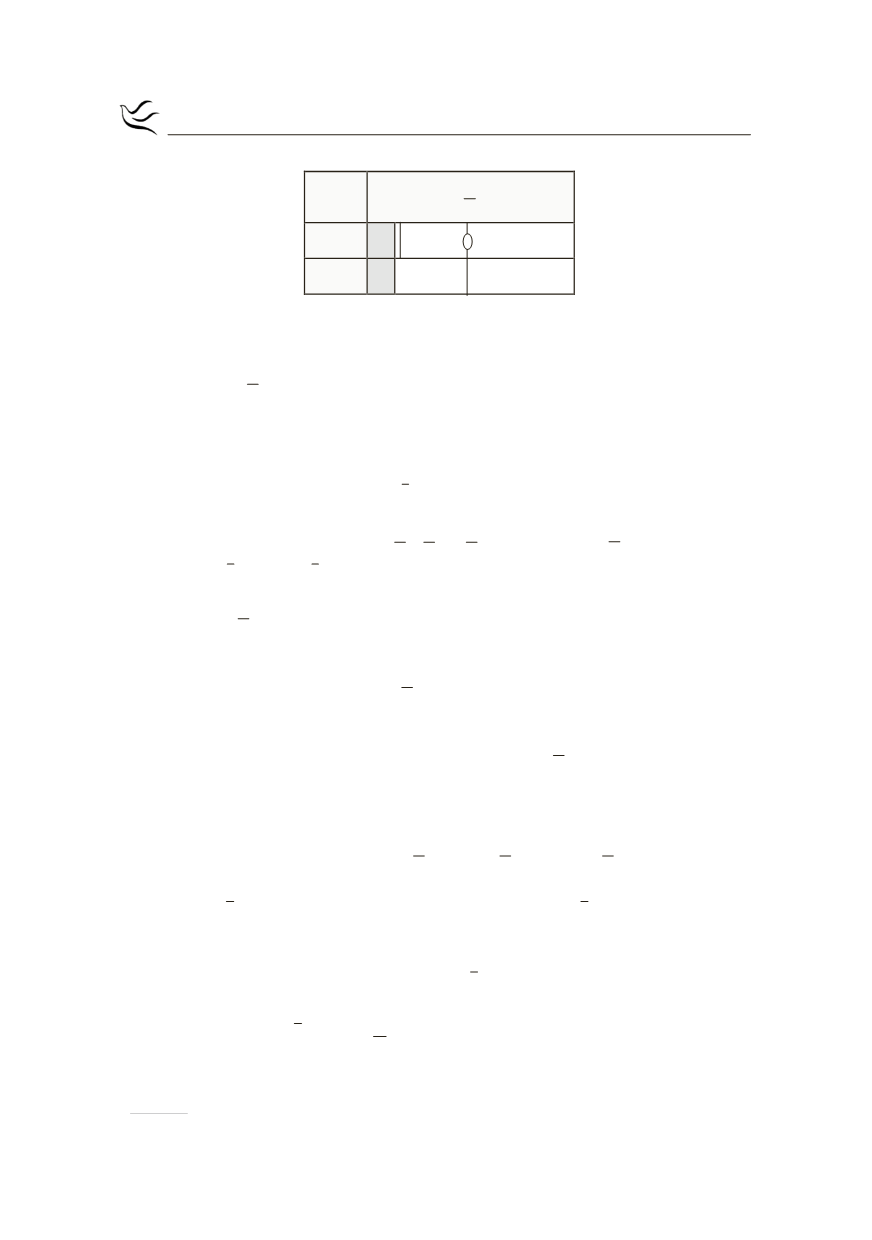
Από τον παραπάνω πίνακα μεταβολών έχουμε:
·
Στο
1
1
Δ 0,
e
é ö
= ÷ êë ø
η
f
είναι γνησίως φθίνουσα και συνεχής άρα
( )
( ) ( )
1
1
x
e
f
Δ lim f x , f 0
-
®
æ
ù
ç
ú
=
ç
ú
è
û
Όμως
( )
(
)
1
1
x
x
e
e
1 1 1
lim f x lim xlnx ln
e e e
-
-
®
®
=
= = -
άρα
( )
1
1
f
Δ
,0
e
æ
ù
= -ç
ú
è
û
·
Στο
2
1
Δ ,
e
é
ö
= +¥ ÷
êë
ø
η
f
είναι γνησίως αύξουσα και συνεχής άρα
( )
2
x
1
f
Δ f
, lim f(x)
e
®+¥
é
ö
æ ö
=
÷
ç ÷ ê
è ø ë
ø
Όμως,
( )
(
)
x
x
lim f x lim xlnx
®+¥
®+¥
=
= +¥
άρα
( )
2
1
f
Δ
,
e
é
ö
= - +¥ ÷
êë
ø
.
Επομένως ,το σύνολο τιμών της
f
θα είναι:
( ) ( ) ( )
f
1
2
1
1
1
f D f
Δ f Δ
, 0
,
,
e
e
e
æ
ù é
ö é
ö
= È = - È - +¥ = - +¥
ç
÷
÷
ú ê
ê
è
û ë
ø ë
ø
.
γ.
Επειδή
α
x
e 0
>
, για κάθε
x 0
¹
, για την εξίσωση
α
x
x e
=
προκύπτει ο περιο-
ρισμός
(
)
x 0,
Î +¥
.
Με τον περιορισμό αυτό η εξίσωση
α
x
x e
=
γράφεται ισοδύναμα:
α
x
α
lnx ln e lnx
xlnx
α f(x) α
x
= Û = Û = Û =
,
x 0
>
(1)
x
0
1
e
+¥
( )
f x
¢
-
+
f
> 1









