Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
196
·
( )
(
)(
)
f x 0 3 x 1 x 1 0 x 1
ή x 1
¢
> Û - + > Û < - >
·
( )
(
)(
)
f x 0 3 x 1 x 1 0 1 x 1
¢
< Û - + < Û- < <
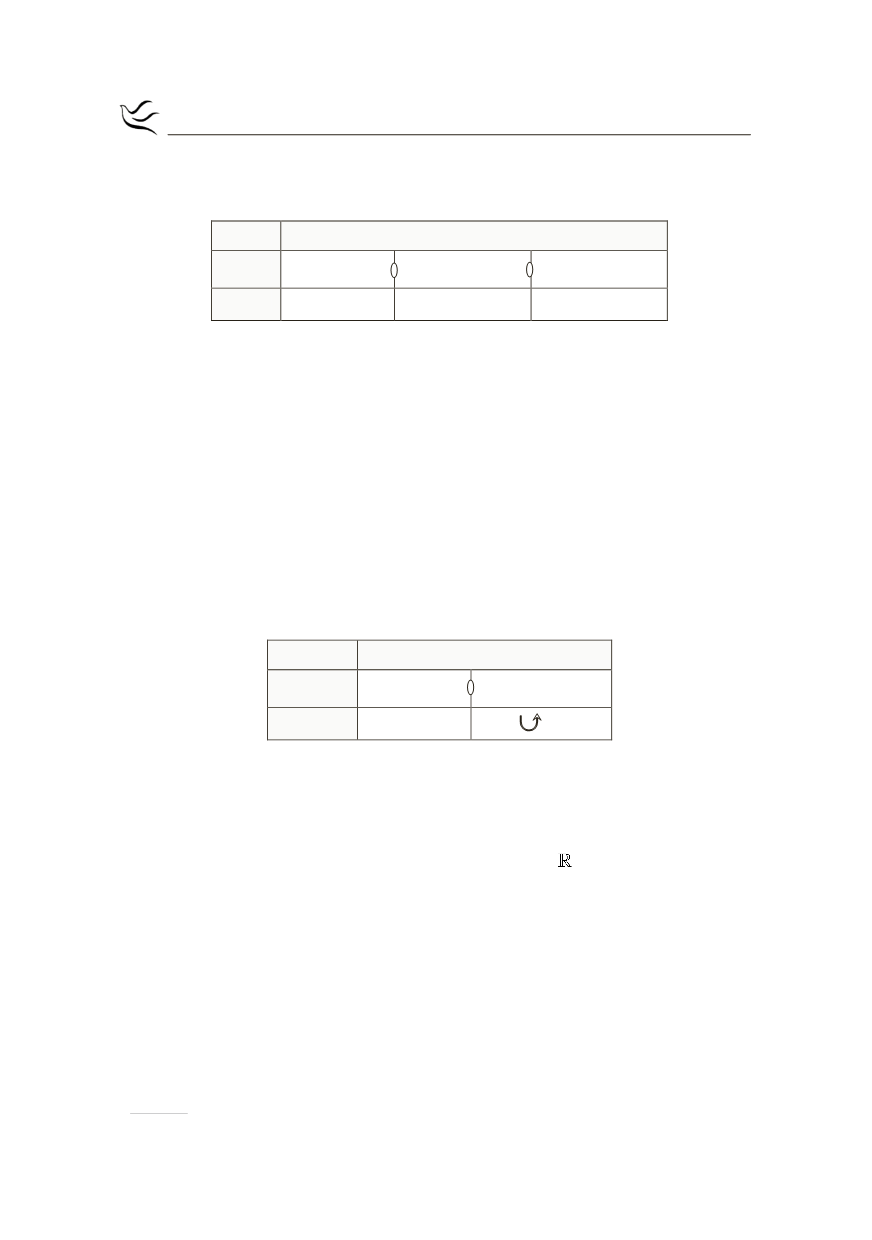
Από τον παραπάνω πίνακα μεταβολών έχουμε ότι
·
έχει τοπικό μέγιστο στο
1
x 1
= -
, το
( )
2
f 1 2
συν θ 0
- =
>
·
έχει τοπικό ελάχιστο στο
2
x 1
=
, το
( )
(
)
2
f 1 2 1
ημ θ
= - +
Για να υπολογίσουμε το σημείο καμπής θα υπολογίσουμε την
f
¢¢
και το
πρόσημό της.
Έτσι :
( )
f x 6x
¢¢
=
.
Οπότε
( )
f x 0 6x 0 x 0
¢¢
= Û = Û =
και
·
( )
f x 0 6x 0 x 0
¢¢
> Û > Û >
·
( )
f x 0 6x 0 x 0
¢¢
< Û < Û <
Η f έχει σημείο καμπής το
( )
(
)
Γ 0,f 0
δηλαδή
(
)
2
Γ 0, 2ημ θ
-
(
αφού η
f
¢¢
αλ-
λάζει πρόσημο εκατέρωθεν του μηδενός και ορίζεται εξίσωση εφαπτομένης
στο σημείο αυτό αφού η
f
είναι παραγωγίσιμη στο
άρα και στο 0).
β.
• Η f είναι γνησίως αύξουσα και συνεχής στο
(
]
1
Δ
, 1
= -¥ -
άρα:
( )
( ) ( )
(
1
x
f
Δ lim f x ,f 1
®-¥
ù
=
-
û
Όμως,
( )
3
x
x
lim f(x) lim x
®-¥
®-¥
=
= -¥
και
2
f( 1) 2
συν θ 0
- =
>
Οπότε,
( )
(
2
1
f
Δ
,2συν θ
ù
= -¥ û
x
-
¥
-1 1
+
¥
( )
f x
¢
+
-
+
f
1
>
1
x
-
¥
0
+
¥
( )
f x
¢¢
-
+
f
l
o









