Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
198
(
)
(
)
2
2
2 1
ημ θ 2 1 ημ θ
Û- + = - +
Για το σημείο Γ:
( )
2
2
2
y 2x 2
ημ θ 2ημ θ 2 0 2ημ θ
= - - Û- = - -
2
2
2
ημ θ 2ημ θ
Û- = -
δ.
Βρίσκουμε τα κοινά σημεία των
C
f
, ε:
( )
3
2
2
3
f x y x 3x 2
ημ θ 2x 2ημ θ x x 0
= Û - - = - - Û - =
(
)(
)
x x 1 x 1 0 x 0
ή x 1 ή x 1
Û - + = Û = = - =
Επομένως, το ζητούμενο εμβαδόν Ε του χωρίου είναι:
( )
(
)
1
1
1
3
2
2
3
-1
-1
-1
E f x y dx x 3x 2
ημ θ 2x 2ημ θ dx x x dx
=
- = - - - - -
= -
ò
ò
ò
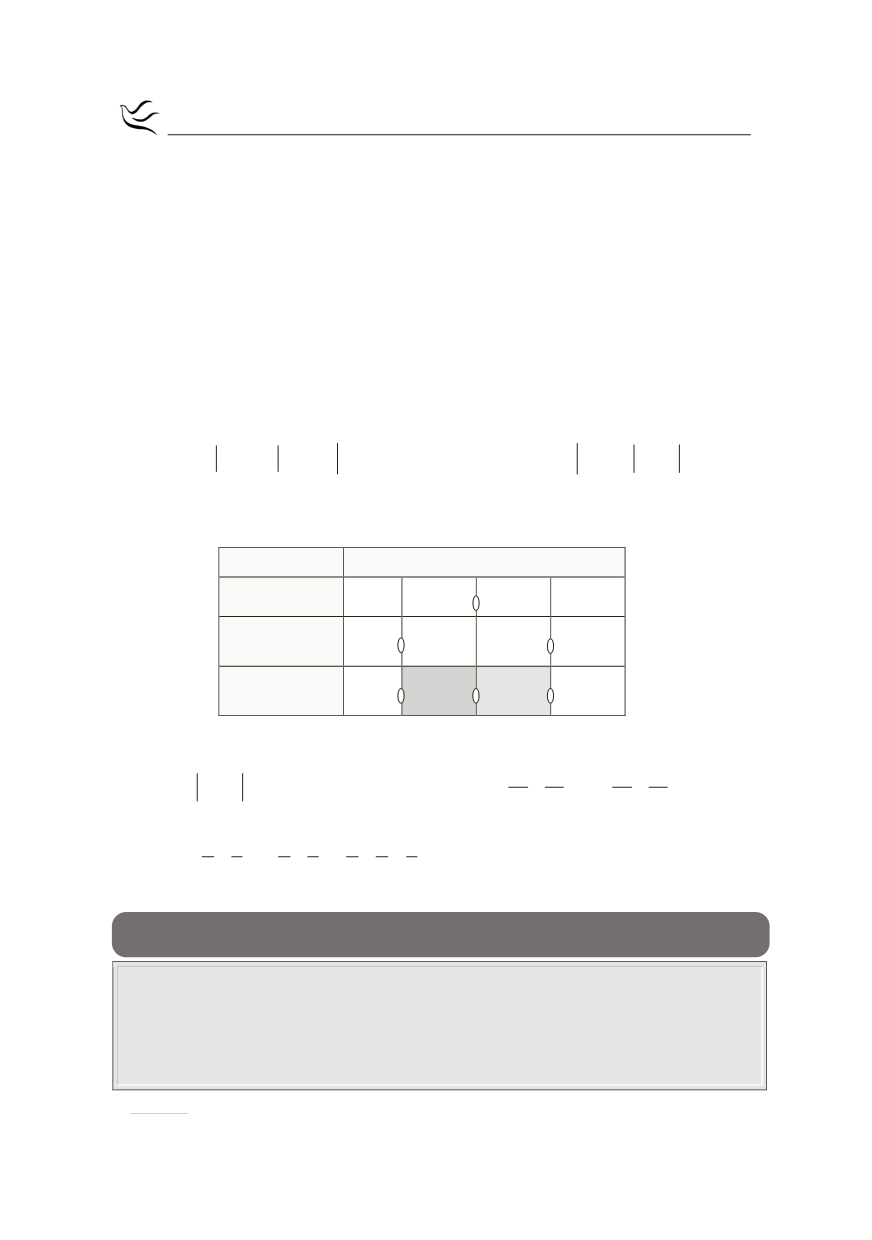
Το πρόσημο της παράστασης
(
)
3
2
x x x x 1
- = -
φαίνεται στον παρακάτω
πίνακα:
Έτσι,
το ολοκλήρωμα γίνεται:
(
)
(
)
0
1
4
2
4
2
1
0
1
3
3
3
-1
-1
0
1
0
x x
x x
E x x dx
x x dx x x dx=
4 2
4 2
-
é
ù é
ù
= - = - - -
- - -
ê
ú ê
ú
ë
û ë
û
ò
ò
ò
1 1 1 1 1 1 1
τ.μ.
4 2 4 2 4 4 2
æ
ö æ
ö
= - + - - = + =
ç
÷ ç
÷
è
ø è
ø
Δίνεται η συνάρτηση
( )
xlnx, x 0
f x
0 , x 0
>
ì
= í
=
î
α.
Να αποδείξετε ότι η συνάρτηση f είναι συνεχής στο 0.
(Μονάδες 3)
x
-¥
-1 0
1
+¥
x
-
-
+
+
2
x 1
-
+
-
-
+
3
x x
-
-
+
-
+
ΘΕΜΑ Γ
ΠΑΝΕΛΛΑΔΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2008









