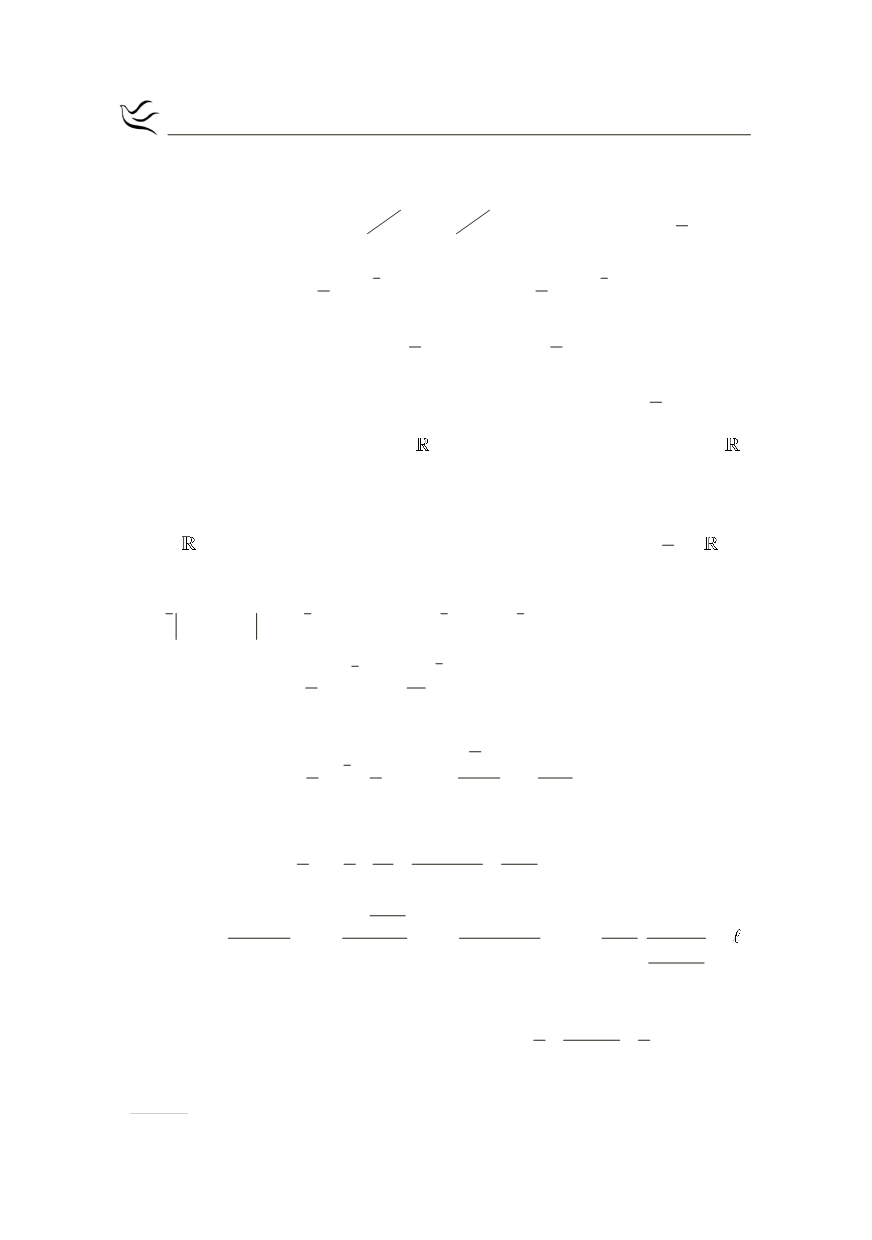
Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
192
Για να διέρχεται η (ε) από την αρχή των αξόνων αρκεί
να επαληθεύεται
από τις συντεταγμένες του σημείου Ο(0,0) δηλαδή:
(
)
0
0
0
λx
λx
λx
0
0 e
λe 0 x
e
- =
- Û -
0
λx
0
x
λ e
= -
λx 0
0
e
0
0
1
1
λ( x ) x
λ
¹
Û - = - Û =
.
Επομένως
( )
æ ö = = =
ç ÷
è ø
1
λ
λ
0
1
f x f
e e
λ
και
( )
æ ö
¢
¢= = =
ç ÷
è ø
1
λ
λ
0
1
f x f
λe λe
λ
.
Έτσι η (ε) γίνεται:
1
1
y e
λe x
y λex λe e y λex
λ
λ
æ
ö
- = - Û = - + Û =
ç
÷
è
ø
.
Οι συντεταγμένες του σημείου επαφής
( )
(
)
0
0
M x , f x
είναι
1
M ,e
λ
æ ö
ç ÷
è ø
.
γ.
Η συνάρτηση
f
είναι κυρτή στο
αφού
( )
¢¢
= >
2
λx
f x
λ e 0
για κάθε
x
Î
επομένως η γραφική παράσταση της
f
είναι πάνω από την εξίσωση της
εφαπτομένης της με εξαίρεση το σημείο επαφής
άρα
( )
³
f x
λex
για κάθε
x
Î
.
Επιπλέον
,
η συνάρτηση
( )
-
f x
λex
είναι συνεχής στο
1
0,
λ
é ù Í ê ú ë û
ως
διαφορά συνεχών συναρτήσεων οπότε
το ζητούμενο εμβαδόν
είναι
( )
(
)
1
1
1
1
λx
λx
λ
λ
λ
λ
0
0
0
0
f x
λex dx e λex dx e dx λexdx
-
= -
=
-
ò
ò
ò
ò
1
1
2
λ
λ
λx
0
0
1
x
e
λe
λ
2
é
ù
é
ù
=
- ê
ú
ê
ú
ë
û ë
û
( )
2
2
1
λ
0
λ
1
0
1
1
λ
e e
λe
λe
λ
λ
2
2
æ
ö
æ ö
ç
÷
ç ÷
æ
ö
è ø
ç
÷
= ×
- -
-
ç
÷ ç
÷
è
ø ç
÷
è
ø
1 1 e 2e 2 e e 2
e
λ λ 2λ 2λ
2λ
- - -
= × - - =
=
δ.
Είναι
( )
(
)
(
)
2
2
λ
λ
λ
λ
e 2
λ
λ E λ
e 2 λ
e 2 1
2
λ
lim
lim
lim
lim
2
ημλ
2
ημλ
2 ημλ
2 2 ημλ
2
λ
®+¥
®+¥
®+¥
®+¥
-
æ
ö
×
ç
÷
×
-
-
=
=
=
×
=
ç
÷
+
+
+
+
ç
÷
è
ø
Για
λ Μ
>
με Μ μεγάλος θετικός αριθμός είναι:
1
ημλ 1
- £ £ Û
1 2
ημλ 3
£ + £ Û
1 2
ημλ 3
0
λ λ λ
+
< £
£









