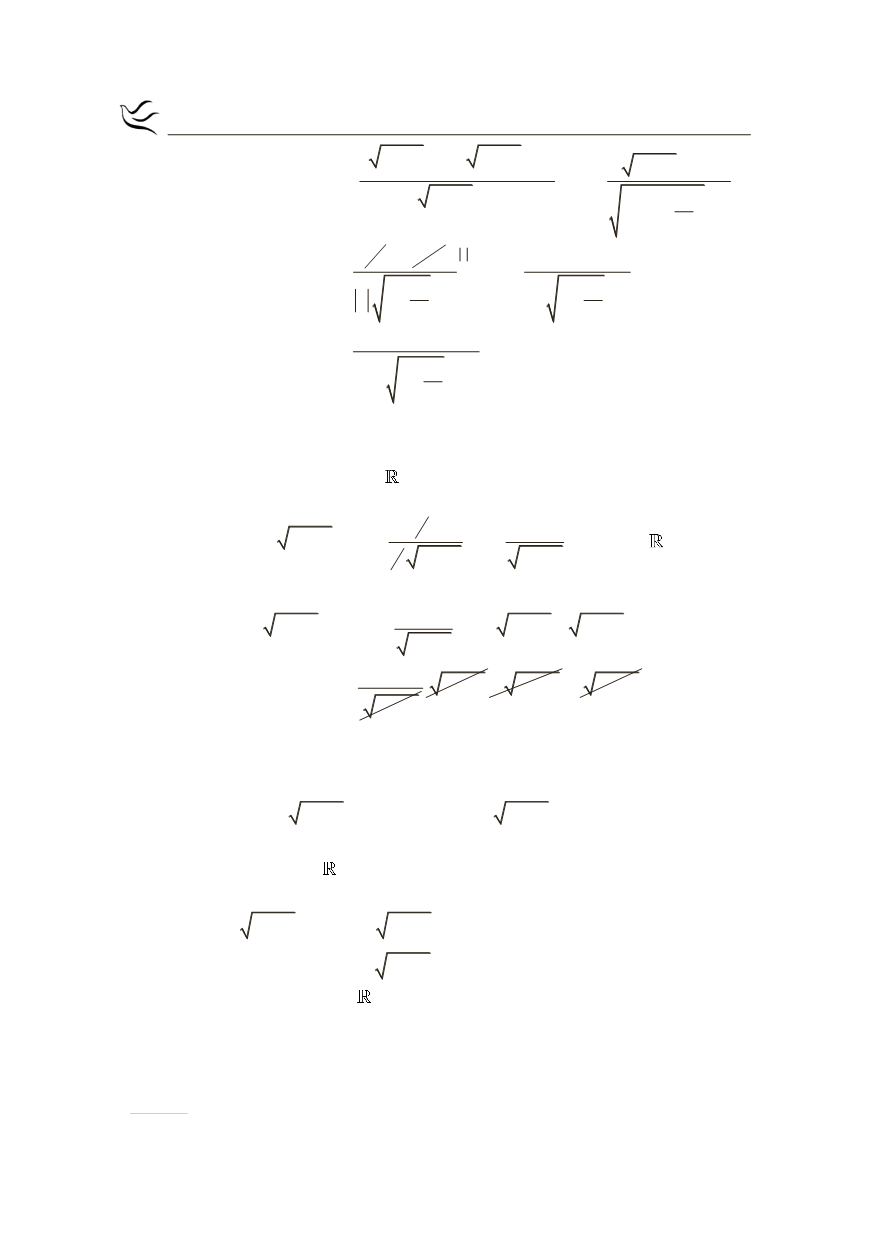
Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
188
(
)(
)
2
2
2
2
2
2
x
x
2
2
x 1 x x 1 x
x 1 x
lim
lim
1
x 1 x
x 1
x
x
®-¥
®-¥
+ -
+ +
+ -
=
=
+ -
æ
ö + -
ç
÷
è
ø
2
x
x
lim
®-¥
=
2
1 x
+ -
x x
x
2
2
1
lim
1
1
x 1
x
x 1
x
x
x
=-
®-¥
=
=
+ -
- + -
x
2
1
lim
0
1
x 1
1
x
®-¥
=
=
æ
ö
- + +
ç
÷
è
ø
Οπότε
,
η πλάγια ασύμπτωτη της γραφικής παράστασης της
f
στο
-¥
εί-
ναι η ευθεία
:
y 2x
= -
γ.
Η
f
είναι παραγωγίσιμη στο
ως διαφορά παραγωγίσιμων συναρτήσεων
με:
( )
(
)
2
2
f x
x 1 x
¢
¢
= + - =
x
2
2
2
x
1
1
x 1
x 1
- =
-
+
+
με
x
Î
Τότε έχουμε:
( )
( )
2
2
2
2
x
f x x 1 f x
1 x 1 x 1 x
x 1
æ
ö
¢
×
+ + =
- ×
+ + + -
ç
÷
+ è
ø
2
x
x 1
=
+
2
x 1
+
2
x 1
- +
2
x 1
+ +
x x x 0
- = - =
δ.
Από το
γ.
ερώτημα έχουμε
( )
( )
( )
( )
2
2
f x x 1 f x 0 f x x 1 f x
¢
¢
×
+ + = Û ×
+ = -
(1)
Έστω ότι υπάρχει
ρ
Î
,
ώστε
( )
2
2
f
ρ 0 ρ 1 ρ 0 ρ 1 ρ
= Û + - = Û + = Û
2
2
2
2
2
ρ 1 ρ ρ 1 ρ 1 0
Û + = Û + = Û =
Άτοπο
Άρα
,
( )
f x 0
¹
για κάθε
x
Î
.
Τότε θα είναι
:









