Μαθηματικά Γ' Λυκείου

155 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
154
Για >
x 1 : ( ) >
¢ = - Û- = - Û = Û =
x 1
2
2
1 1 1
f x x 4 x 2
4 x 4
Άρα τα σημεία που η εφαπτομένη της f C είναι παράλληλη στην ευθεία
= - +1
y x 2018
4
είναι τα
æ ö æ ö
- -
ç ÷ ç ÷
è ø è ø
1 1
A ,f
8 8
και ( ) ( )
B 2,f 2
Έχουμε
æ ö - = ç ÷
è ø
æ ö ¢ - =- ç ÷
è ø
æ ö æ öæ ö æ ö
¢ - - = - + Û - = - + Û = - +ç ÷ ç ÷ç ÷ ç ÷
è ø è øè ø è ø
1 65
f
8 64
A 1 1
f
8 4
1 1 1 65 1 1 1 63
ε : y f f x y x y x
8 8 8 64 4 8 4 64
( ) ( )( )
( )
( )
( )
=
¢ =-
¢ - = - Û - = - - Û = - +
3
f 2
2
B 1
f 2
4
3 1 1
ε : y f 2 f 2 x 2 y x 2 y x 2
2 4 4
Β4. Η f είναι συνεχής στο h άρα δεν έχει κατακόρυφες ασύμπτωτες.
Ωστόσο έχουμε,
( )
®+¥ ®+¥ ®+¥ ®+¥ ®+¥
+
+
= = = = =
2 2
x x x x x
x 1
f x x 1 x 1
x
lim lim lim lim lim 0
x x x x x
( )
®+¥ ®+¥ ®+¥ ®+¥
+
= = = =
x x x x
x 1 x
lim f x lim lim lim 1 1
x x
Άρα η ευθεία =
y 1 οριζόντια ασύμπτωτη της f C στο +¥
Στο -¥ η f είναι πολυωνυμική συνάρτηση 2ου βαθμού άρα δεν έχει πλάγιες
ή οριζόντιες ασύμπτωτες.
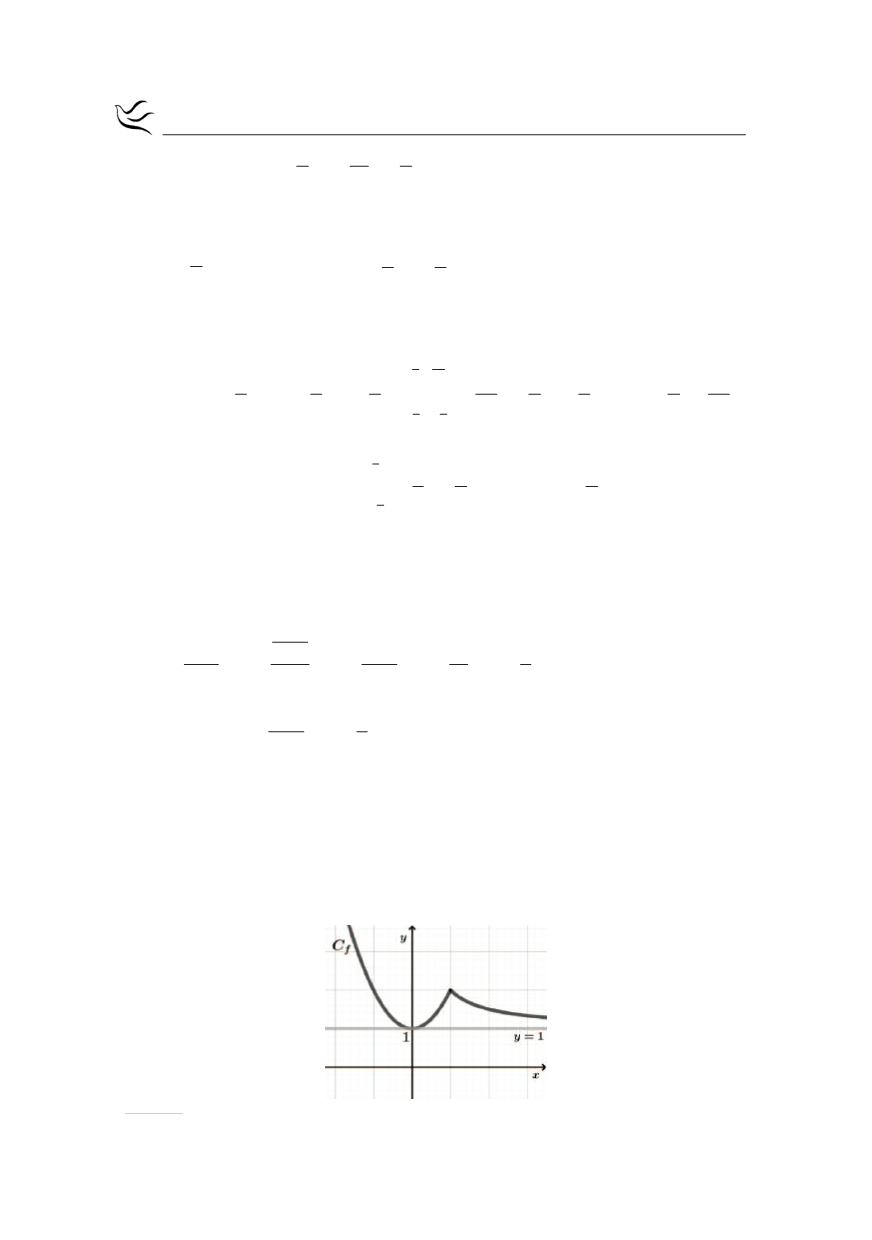
Η γραφική παράσταση της f φαίνεται παρακάτω