151
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Α1.
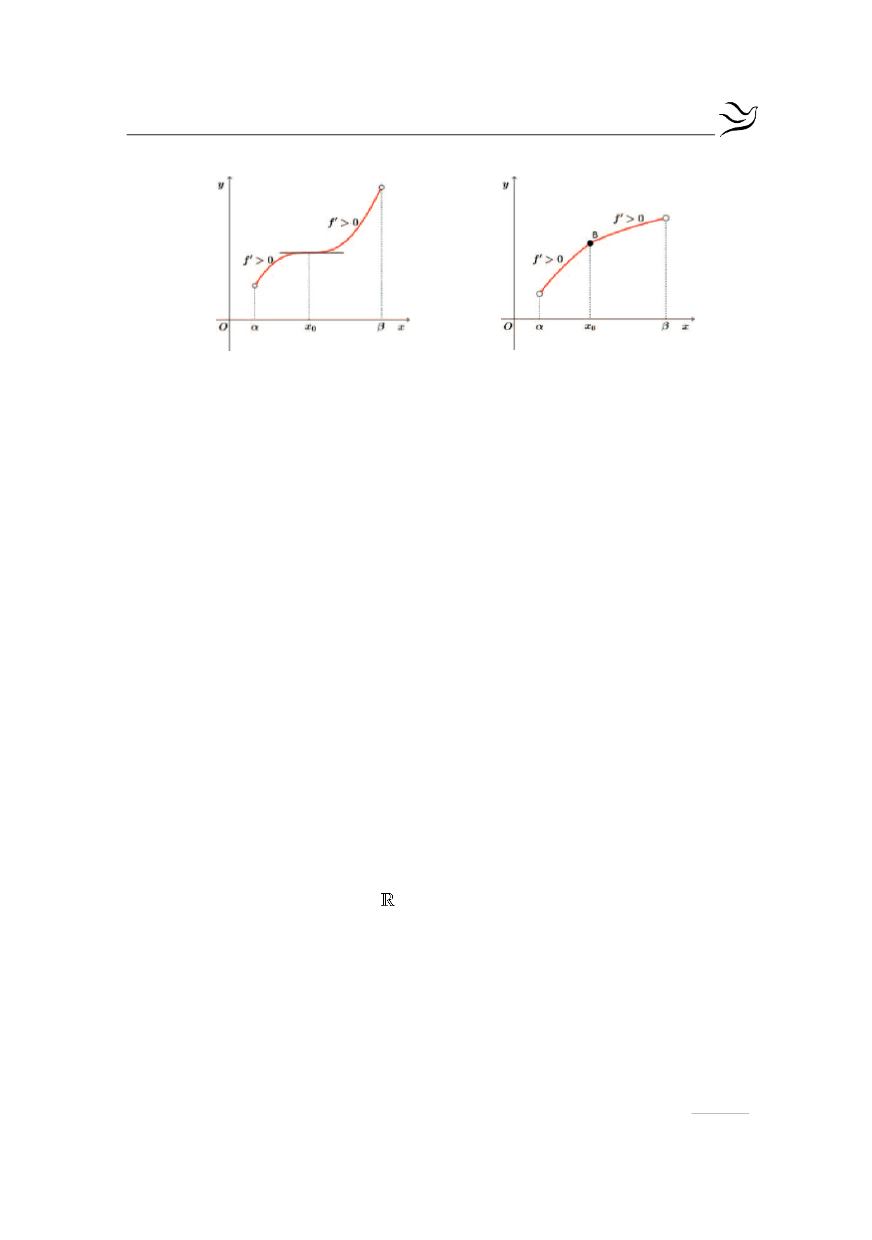
Έστω ότι
( )
f x 0
¢
>
, για κάθε
(
) (
)
0
0
x
α,x
x ,β
Î È
.
Επειδή η f είναι συνεχής στο
0
x
θα είναι γνησίως αύξουσα σε κάθε ένα από
τα διαστήματα
(
]
0
α,x
και
[
)
0
x ,
β
. Επομένως, για
1
0
2
x x x
< <
ισχύει
( ) ( ) ( )
1
0
2
f x f x f x
< <
. Άρα το
( )
0
f x
δεν είναι τοπικό ακρότατο της f. Θα δεί-
ξουμε, τώρα, ότι η f είναι γνησίως αύξουσα στο
( )
α,β
. Πράγματι, έστω
( )
1 2
x ,x
α,β
Î
με
1
2
x x
<
.
P
Αν
(
]
1 2
0
x ,x
α,x
Î
, επειδή η f είναι γνησίως αύξουσα στο
(
]
0
α,x
, θα ισχύει
( ) ( )
1
2
f x f x
<
.
P
Αν
[
)
1 2
0
x ,x x ,
β
Î
, επειδή η f είναι γνησίως αύξουσα στο
[
)
0
x ,
β
, θα ισχύει
( ) ( )
1
2
f x f x
<
.
P
Τέλος, αν
1
0
2
x x x
< <
, τότε
( ) ( ) ( )
1
0
2
f x f x f x
< <
.
Επομένως, σε όλες τις περιπτώσεις ισχύει
( ) ( )
1
2
f x f x
<
, οπότε η f είναι
γνησίως αύξουσα στο
( )
α,β
.
Ομοίως, αν
( )
f x 0
¢
<
για κάθε
(
) (
)
0
0
x
α,x
x ,β
Î È
.
Α
2.
Έστω Α ένα υποσύνολο του . Ονομάζουμε πραγματική συνάρτηση με πε-
δίο ορισμού το Α
μια διαδικασία (κανόνα) f, με την οποία κάθε στοιχείο
x A
Î
αντιστοιχίζεται σε ένα μόνο πραγματικό αριθμό y. Το y ονομάζεται
τιμή της f στο x
και συμβολίζεται με
( )
f x
.
Α
3.
Η παράγωγος της
f
μπορεί να είναι η Τ.
Η παράγωγος της
g
μπορεί να είναι η Η.









