Μαθηματικά Γ' Λυκείου

148 / 368

147
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
● ( ) ( ) x
x α x
α α x
x x x x
e 2 x
lim f x lim 2e 2x lim 2 2x lim e 2 L
e e e
-
®+¥ ®+¥ ®+¥ ®+¥
æ ö é ù æ ö
¢ = - = - = - =
ç ÷ ç ÷ ê ú
è ø ë û è ø
x x
x x
x 1
lim lim 0
e e
+¥
+¥
®+¥ ®+¥
= = άρα L =+¥
Αφού α 1 2α 2 2 2α 0> Û > Û - < έχουμε ότι ( )1 0 f Δ ¢Î , ( )2 0 f Δ ¢Î και ε-
πειδή η f΄ είναι 1-1 σε κάθε ένα από τα διαστήματα
1 Δ , 2 Δ υπάρχει ακριβώς
ένα 1 1 x Δ Î ώστε ( )1 f x 0¢ = και ακριβώς ένα 2 2 x Δ Î ώστε ( )2 f x 0¢ = .
Έτσι λοιπόν έχουμε ότι
Για
( ]
( ) ( ) ( )
f ,α
1 1 x x f x f x f x 0
¢ -¥
¢ ¢ ¢ < Û > Û >
>
Για
( ]
( ) ( ) ( )
f ,α
1 1 x x α f x f x f x 0
¢ -¥
¢ ¢ ¢ < £ Û < Û <
>
Για
( )
( ) ( ) ( ) f α,
2 2 α x x f x f x f x 0
¢ +¥
¢ ¢ ¢ < < Û < Û <
<
Για
( )
( ) ( ) ( )
f α,
2 2 x x f x f x f x 0
¢ +¥
¢ ¢ ¢ > Û > Û >
<
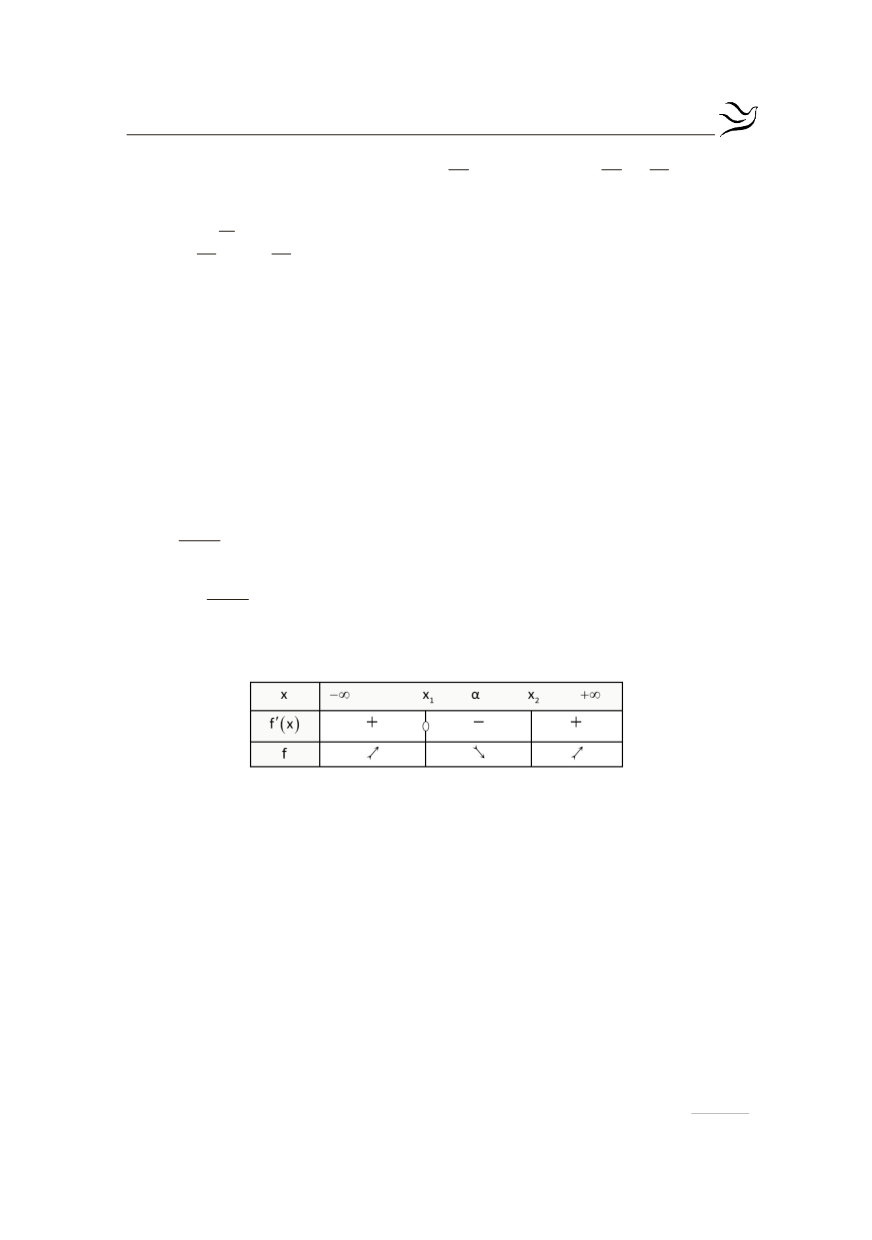
Με τη βοήθεια του παραπάνω πίνακα έχουμε ότι η f παρουσιάζει τοπικό μέ-
γιστο στο 1 x και τοπικό ελάχιστο στο 2 x με 1 2 x x< .
Δ3. Έστω ότι η εξίσωση ( ) ( )
f x f 1= έχει μια ρίζα ( )
2 ρ α,xÎ .
● Η f είναι συνεχής στο [ ]1,ρ
● Η f είναι παραγωγίσιμη στο ( )1,ρ
● ( ) ( )
f ρ f 1=
Ισχύουν οι προϋποθέσεις του θεωρήματος Rolle οπότε υπάρχει τουλάχι-
στον ένα ( )
ξ 1,ρÎ τέτοιο ώστε ( )
f ξ 0 ¢ = .