143
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Είναι
x
4
α x α
4
= Û =
οπότε το εμβαδόν του τετραγώνου είναι
( )
2
2
2
τ
x
x
Ε x α
4 16
æ ö
= = = ç ÷
è ø
,
( )
x 0,8
Î
.
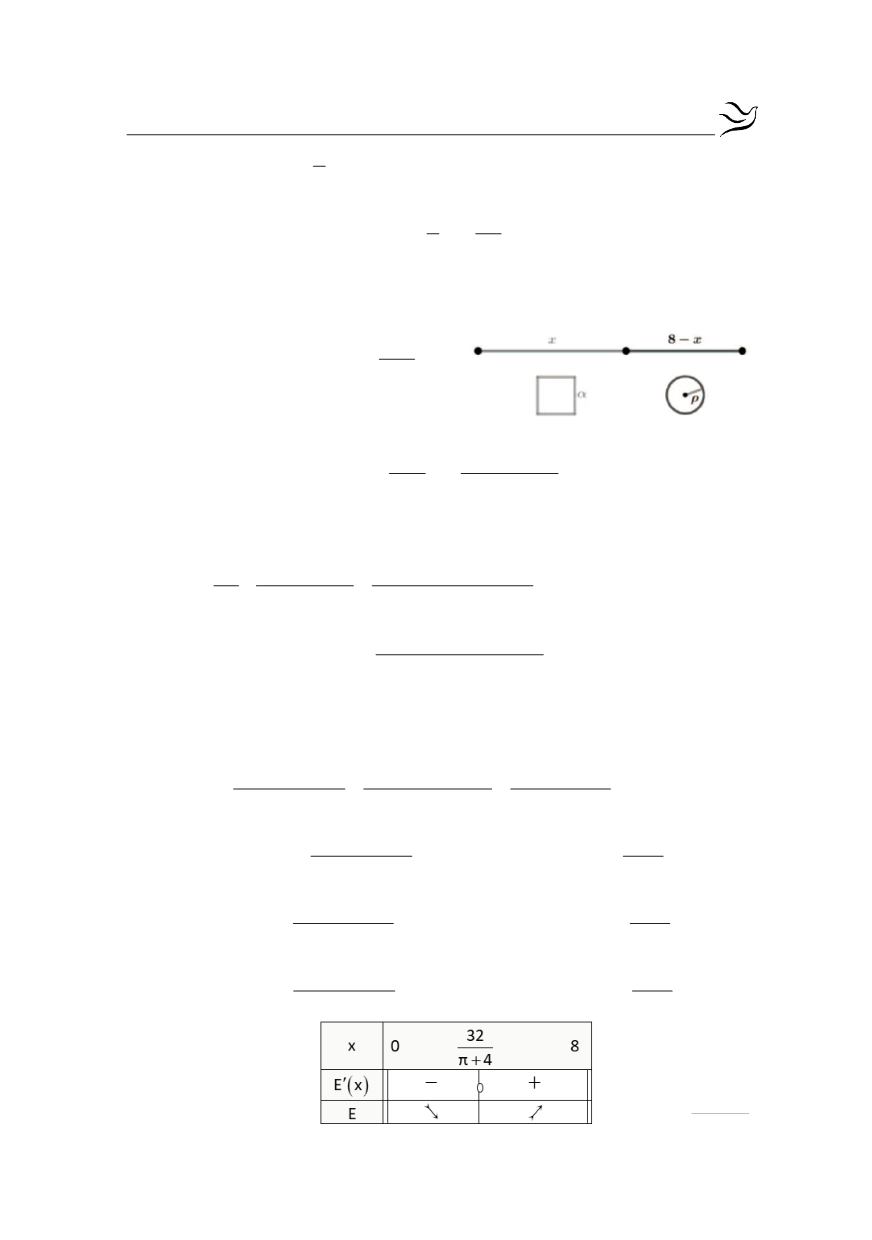
Ας είναι ρ η ακτίνα του κύκλου. Το τμήμα που θα κατασκευάσουμε τον κύ-
κλο είναι
8 x
-
.
Επομένως
8 x
2
πρ 8 x ρ
2
π
-
= - Û =
.
Το εμβαδόν του κύκλου είναι
( )
2
2
2
κ
8 x 64 16x x
Ε x πρ π
2
π
4π
-
- +
æ
ö
= =
=
ç
÷
è
ø
,
( )
x 0,8
Î
.
Τελικά η συνάρτηση που εκφράζει το άθροισμα των εμβαδόν είναι :
( )
2
2
2
2
x 64 16x x
πx 256 64x 4x
Ε x
16
4
π
16π
- +
+ - +
= +
=
(
)
2
π 4 x 64x 256
16
π
+ - +
=
,
( )
x 0,8
Î
.
Γ2.
Η συνάρτηση Ε είναι συνεχής ως πολυωνυμική στο πεδίο ορισμού της και
παραγωγίσιμη με
( ) (
)
(
)
(
)
2
π 4 x 32
2
π 4 x 64
π 4 x 32
Ε x
16
π
16π
8π
é + - ù
+ -
+ -
ë
û
¢
=
=
=
,
( )
x 0,8
Î
Οπότε
( )
(
)
(
)
π 4 x 32
32
Ε x 0
0 π 4 x 32 x
8
π
π 4
+ -
¢
= Û
= Û + = Û =
+
( )
(
)
(
)
π 4 x 32
32
Ε x 0
0 π 4 x 32 8 x
8
π
π 4
+ -
¢
> Û
> Û + > Û > >
+
( )
(
)
(
)
π 4 x 32
32
Ε x 0
0 π 4 x 32 0 x
8
π
π 4
+ -
¢
< Û
< Û + < Û < <
+









