149
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Θέτουμε
2
2
u x 2 x 2 u x u 2
= - Û - = Û = +
άρα
dx 2udu
=
●
Για
x 2
=
είναι
u 0
=
●
Για
x 3
=
είναι
u 1
=
Έτσι λοιπόν
(
)
(
)
(
)
1
1
2
2
2
0
0
Ι
2 u 2 2 u 2udu
2u 2 2u du
é
ù
é
ù
= - + +
= - - ë
û
ë
û
ò
ò
(
)
1
1
5
3
4
2
0
0
4u 4u
4 4 32
4u 4u du
5 3
5 3 15
é
ù
= - -
= - - = - - = -
ê
ú
ë
û
ò
Τελικά,
( )
(
)
3
2
32
f x x 2 dx
15
- > -
ò
.
Α1.
Έστω
f
μια συνάρτηση παραγωγίσιμη σε ένα διάστημα
( )
α,β
με εξαί-
ρεση ίσως ένα σημείο του
0
x
,
στο οποίο όμως η
f
είναι συνεχής. Αν η
( )
f x
¢
διατηρεί πρόσημο στο
(
) (
)
0
0
α,x
x ,β
È
, να αποδείξετε ότι το
( )
0
f x
δεν είναι τοπικό ακρότατο και ότι η
f
είναι γνησίως μονότονη στο
( )
α,β
.
Μονάδες 7
Α
2.
Έστω Α ένα μη κενό υποσύνολο του . Τι ονομάζουμε πραγματική συ-
νάρτηση με πεδίο ορισμού το Α;
Μονάδες
4
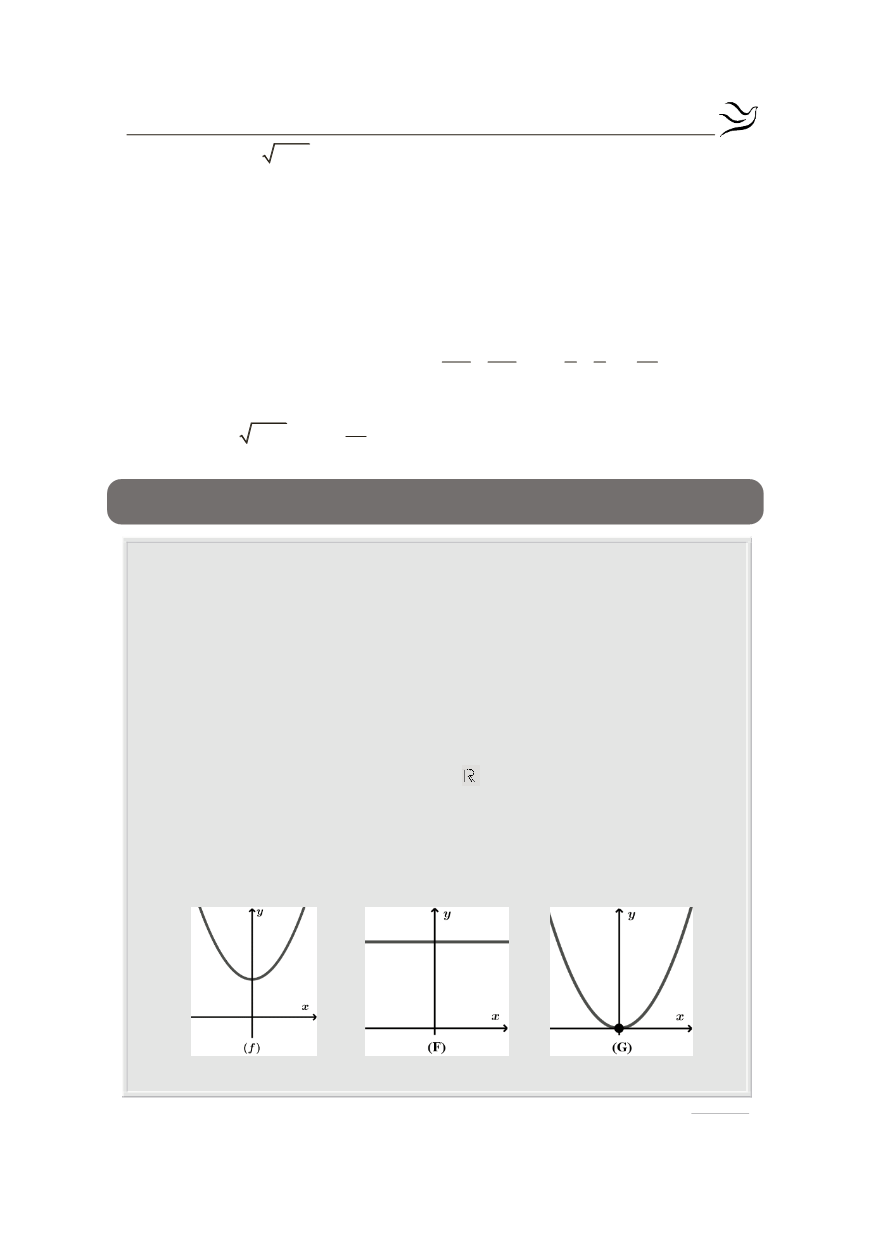
Α3.
Δίνονται οι γραφικές παραστάσεις των συναρτήσεων
f, g, F, G, H, T.
ΘΕΜΑ Α
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΠΑΝΕΛΛΗΝΙΕΣ 2018









