Μαθηματικά Γ' Λυκείου

151 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
150
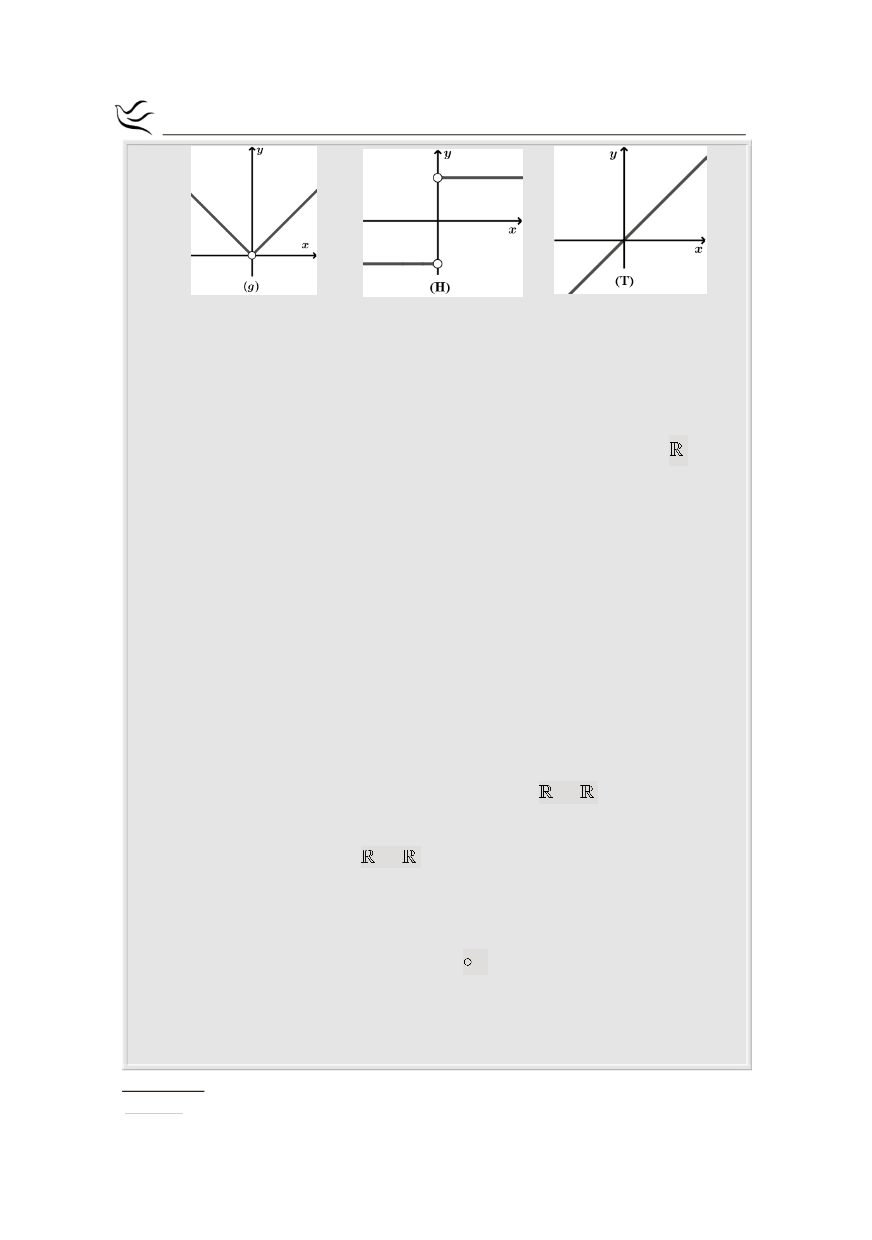
Να γράψετε στο τετράδιό σας ποια από τις συναρτήσεις F, G, H, T μπορεί
να είναι η παράγωγος της συνάρτησης f και ποια της g.
Μονάδες 4
Α4 . Θεωρήστε τον παρακάτω ισχυρισμό:
«Για κάθε ζεύγος πραγματικών συναρτήσεων ( )
f, g : 0, +¥ ® , αν ι-
σχύει ( )
x
lim f x
®+¥
= +¥ και ( )
x
lim g x
®+¥
= -¥ , τότε ( ) ( )
x
lim f x g x 0
®+¥
é + ù =
ë û ».
α) Να χαρακτηρίσετε τον παραπάνω ισχυρισμό γράφοντας στο τετράδιό
σας το γράμμα Α αν είναι αληθής, ή το γράμμα Ψ αν είναι ψευδής.
(Μονάδα 1)
β) Να αιτιολογήσετε την απάντησή σας στο ερώτημα α) (Μονάδες 3)
Μονάδες 4
Α4. Να χαρακτηρίσετε τις προτάσεις που ακολουθούν, γράφοντας στο τετρά-
διό σας, δίπλα στο γράμμα που αντιστοιχεί σε κάθε πρόταση, τη λέξη Σω-
στό αν η πρόταση είναι σωστή, ή Λάθος αν η πρόταση είναι λανθασμένη.
α) Η γραφική παράσταση μιας συνάρτησης f : ® μπορεί να τέμνει
μια ασύμπτωτή της.
β) Αν μια συνάρτηση f : ® είναι «1-1», τότε κάθε οριζόντια ευθεία
τέμνει τη γραφική παράσταση της f το πολύ σε ένα σημείο.
γ) Αν οι συναρτήσεις f και g έχουν πεδίο ορισμού το [ ]0,1 και σύνολο
τιμών το [ ]2,3 , τότε ορίζεται η f g με πεδίο ορισμού το [ ]0,1 και
σύνολο τιμών το [ ]2,3 .
Μονάδες 6
Aπάντηση