Μαθηματικά Γ' Λυκείου

157 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
156
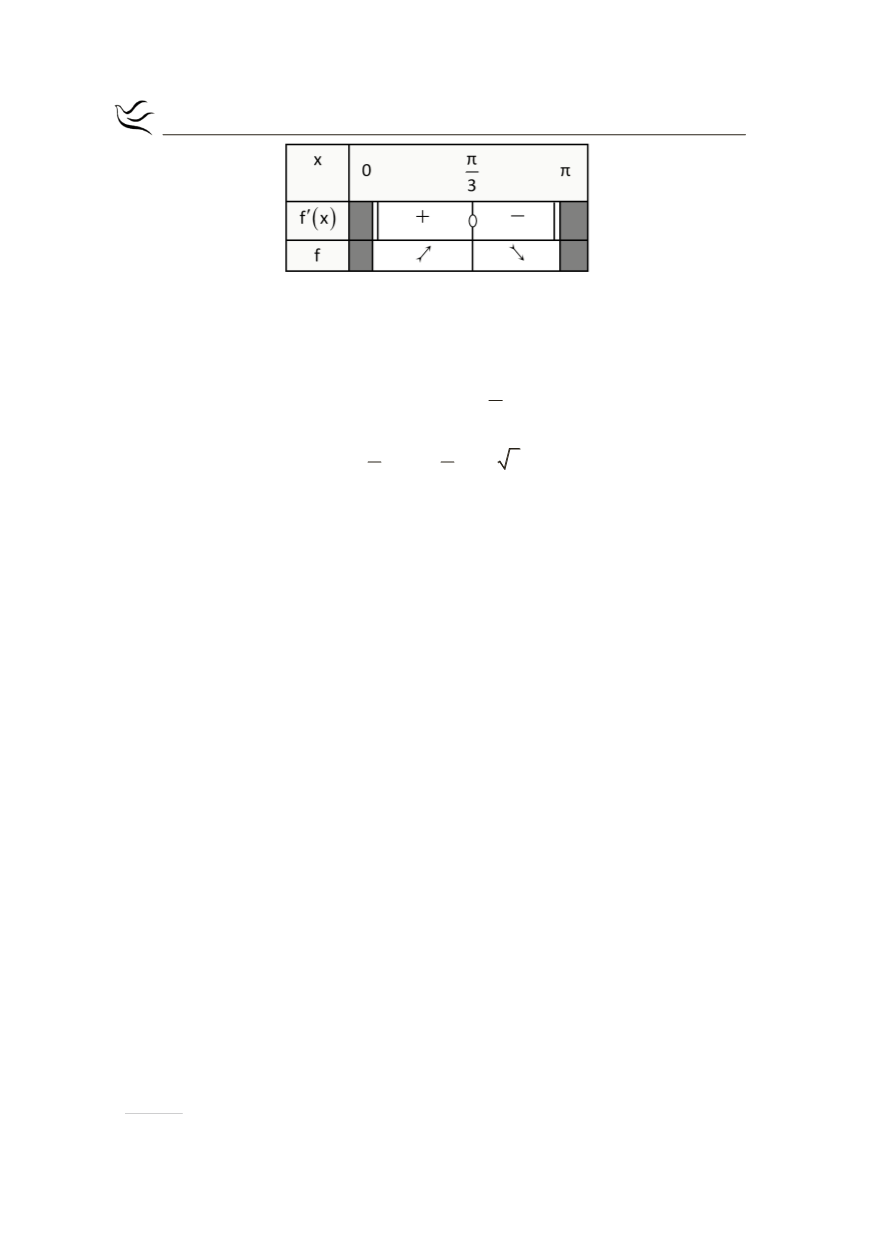
Από τον παραπάνω πίνακα μεταβολών έχουμε ότι:
● Η f παρουσιάζει Τοπικό Ελάχιστο στο 1 x 0= με τιμή ( )
f 0 0= .
● Η f παρουσιάζει Ολικό Μέγιστο στο 2
π
x
3
= με τιμή
π π
f 2ημ 1 3 1
3 3
æ ö = - = -
ç ÷
è ø
.
● Η f παρουσιάζει Τοπικό Ελάχιστο στο 3 x π = με τιμή ( )
f π π= - .
Αφού η f είναι συνεχής στο [ ]0,π από θεώρημα Μέγιστης Ελάχιστης Τιμής
θα παρουσιάζει μέγιστη και ελάχιστη τιμή.
Αφού ( ) ( )
f π π 0 f 0= - < = η f παρουσιάζει Ολικό Ελάχιστο στο 3 x π = .
Γ2. H f είναι παραγωγίσιμη στο [ ]0, π άρα η γραφική της παράσταση δέχεται ε-
φαπτομένη, που ορίζεται ο συντελεστής διεύθυνσής της, σε οποιοδήποτε ση-
μείο ( ) ( )
0 0 Α x ,f x με [ ]
0 x 0, π Î .
Ακόμη, ( )
f x 2ημx 0 ¢¢ = - < για κάθε ( )
x 0, π Î άρα η f είναι κοίλη στο [ ]0,π ο-
πότε η γραφική παράσταση της f βρίσκεται πάνω από την εφαπτομένη της
στο ( ) ( )
0 0 Α x ,f x με εξαίρεση το σημείο επαφής.
Τελικά λοιπόν, για κάθε [ ]
0 x 0, π Î η γραφική παράσταση της f και η εφαπτο-
μένη της στο ( ) ( )
0 0 Α x ,f x έχουν ένα μόνο κοινό σημείο.
Γ3. ( ) ( ) ( ) π π π
0 0 0
Ι f x συνxdx 2ημx x συνxdx 2ημxσυνx xσυνx dx = = - = - ò ò ò
( ) ( ) [ ] ( )
π π π π π
2
0
0 0 0 0
2ημxσυνx dx xσυνx dx ημ x xημx ημxdx é ù = - = - -
ë û ò ò ò
( ) [ ] ( ) [ ]
π π
2 2
0 0
ημ π ημ 0 πημπ συνx συνx συνπ συν0 1 1 2 = - - - - = - = - + = + = .