Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
158
Δ5.
Αν
F
είναι μια αρχική συνάρτηση της
f
στο διάστημα
(
)
0,
+¥
με
( )
F e e ln2
= ×
, να αποδείξετε ότι
( )
e 1
2
ln2 F 1 ln
e 1
+
æ
ö
< < ç
÷ +è
ø
.
Μονάδες 5
A
πάντηση
Δ
1.
Για κάθε
x 0
>
είναι
(
)
(
)
x
x 1 1
ln x 1
ln x 1
x 1
x 1
+ -
+ > Û + >
Û
+
+
(
)
(
)
1
1
ln x 1 1
ln x 1
1
x 1
x 1
Û + > - Û + + >
+
+
(1)
Θεωρούμε
( )
1
g t lnt
t
= +
,
(
)
g
D 0,
= +¥
.
Η
g
είναι παραγωγίσιμη στο
(
)
0,
+¥
με
( )
2
2
1 1 t 1
g t
t t
t
-
¢
= - =
, για
t 0
>
.
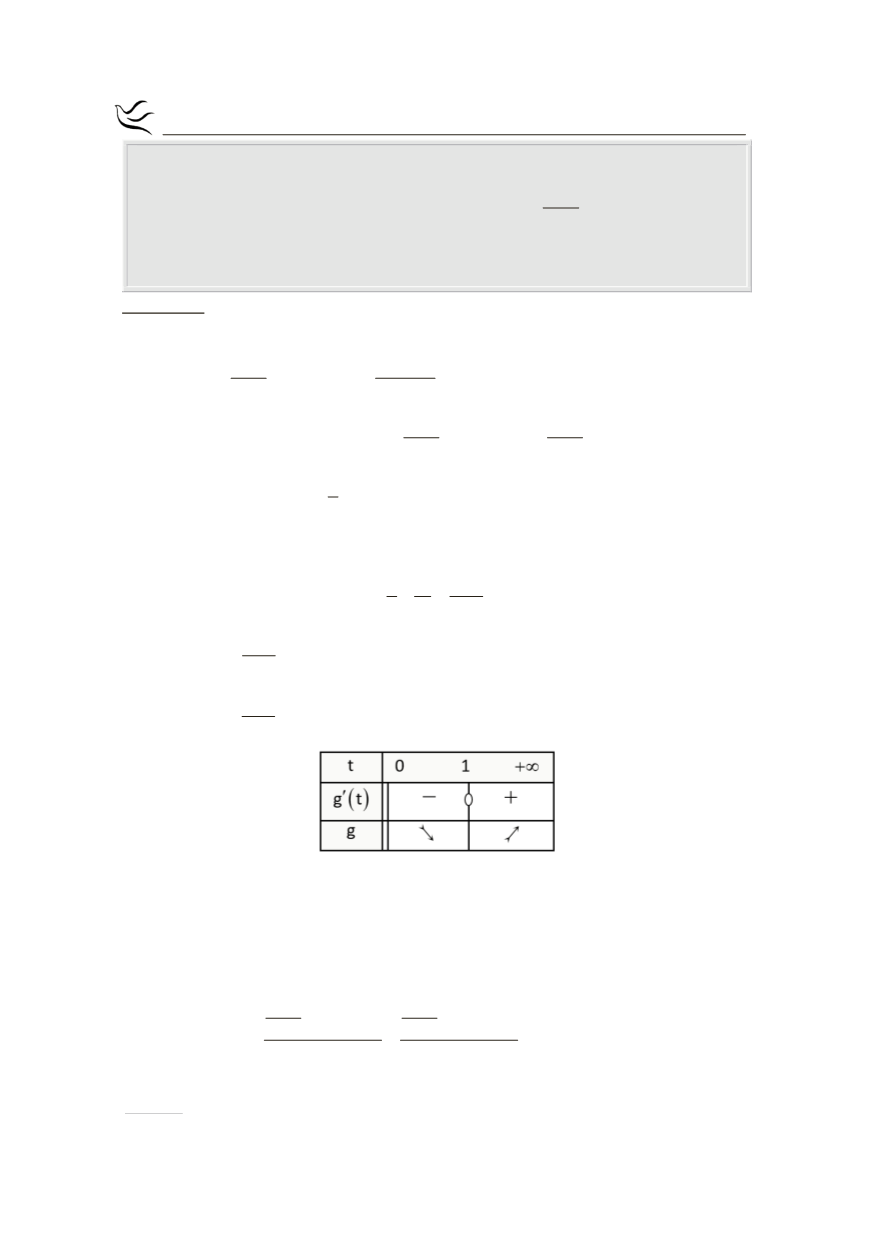
( )
2
t 1
g t 0
0 t 1 0 t 1
t
-
¢
= Û = Û - = Û =
( )
2
t 0
2
t 1
g t 0
0 t 1 0 t 1
t
>
-
¢
> Û > Û - > Û >
Η
(1)
(
) ( )
[
)
(
)
[
)
x 1 1,
1 1,
g 1,
g x 1 g 1
x 1 1 x 0
+ Î +¥
Î +¥
+¥
Û + >
Û + > Û >
<
που ισχύει.
Δ
2.
Η
f
είναι παραγωγίσιμη στο
(
)
0,
+¥
με
( )
(
)
(
)
2
2
x
x
ln x 1
ln x 1
x 1
x 1
f x
0
x
x
- +
- +
+
+
¢
=
=
<
για κάθε
x 0
>









