Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
136
Άρα η
g
είναι γνησίως αύξουσα στο
é
ù -ê
ú
ë
û
π
,0
2
.
Παρατηρούμε ότι
( )
=
g 0 0
.
( )
( ) ( )
-
= Û = Û =
g:1 1
g x 0 g x g 0 x 0
Για
( ) ( )
( )
é
ù -ê
ú
ë
û
- < < Û < Û <
π
g
,0
2
π
x 0
g x g 0 g x 0
2
1
Για
(
)
Î +¥
x 0,
:
( )
¢
= -
2
f x 3x 6x
( )
(
)
>
¢
= Û - = Û - = Û =
3x 0
2
f x 0 3x 6x 0 3x x 2 0 x 2
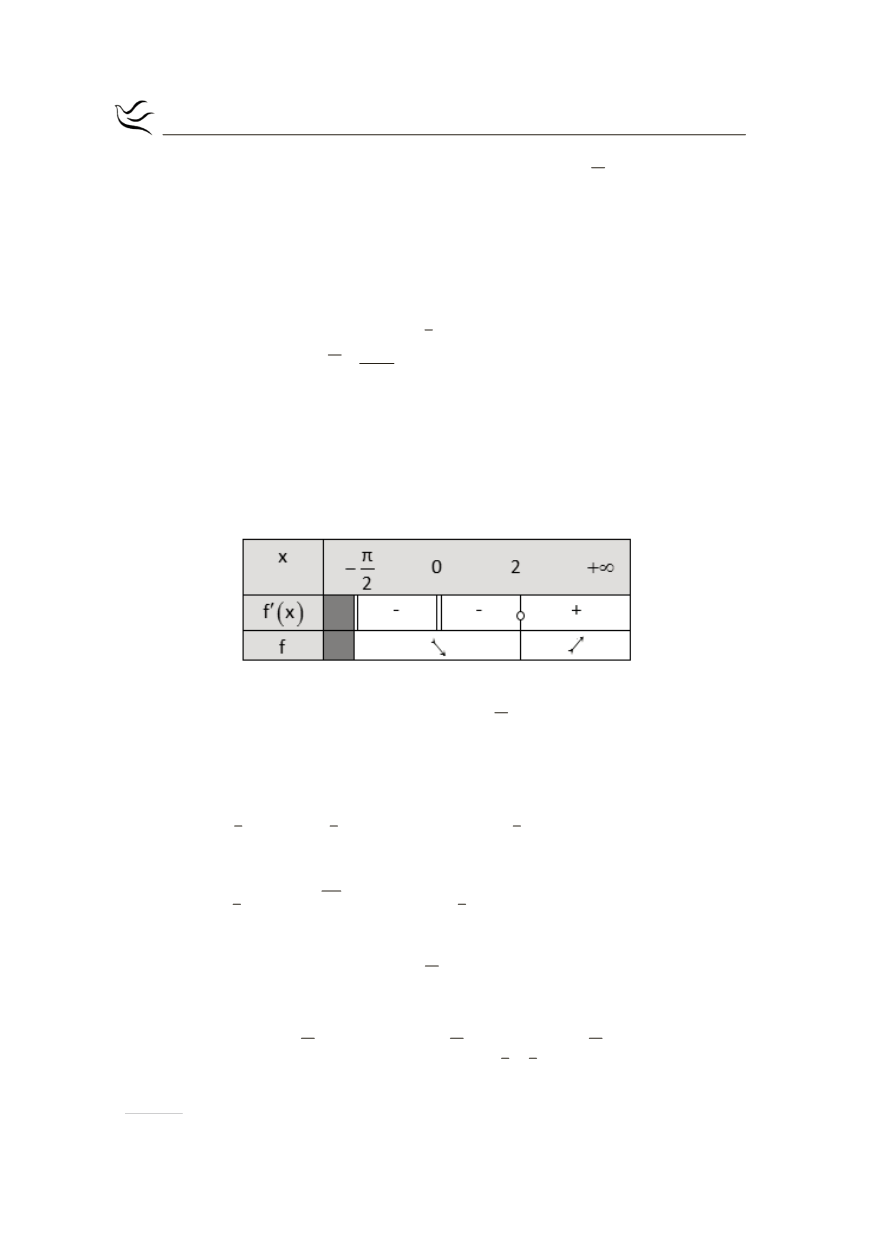
Τελικά λοιπόν έχουμε τον παρακάτω πίνακα μεταβολών
Οπότε η
f
είναι γνησίως φθίνουσα στο
é
ù -ê
ú
ë
û
π
,2
2
και γνησίως αύξουσα στο
[
)
+¥
2,
.
Δ4.
Είναι
( )
( )
( )
( )
(
)
2
0
2
0
2
3
2
π
π
π
0
0
2
2
2
Ι
f x dx
f x dx f x dx
f x dx x 3x 2 dx
-
-
-
=
=
+
=
+ - +
ò
ò
ò
ò
ò
( )
( )
2
4
0
0
3
π
π
2
2
0
x
f x dx
x 2x
f x dx
4
-
-
é
ù
=
+ - + =
ê
ú
ë
û
ò
ò
Η
f
είναι γνησίως φθίνουσα στο
π
,0
2
é
ù -ê
ú
ë
û
και συνεχής οπότε
( )
( )
f 0 2
π 2
f
3
2
π
π
π
2
f
,0 f 0 , f
2,
3
2
2
π
=
æ ö - =- +
ç ÷
è ø
æ
ö é
ù
é
ù
æ ö
é
ù
-
=
-
=
- +
ç
÷
ç ÷
ê
ú
ê
ú
ê
ú
ë
û
è ø
ë
û
è
ø ë
û









