129
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
Β4.
Να εξετάσετε αν υπάρχει
[ ]
0
x 0,2
Î
για το οποίο το εμβαδόν
( )
0
f x
του
αντίστοιχου τετραγώνου ΕΖΗΘ ισούται με
0
x
4e 1
+
2
cm
.
Μονάδες 6
A
πάντηση
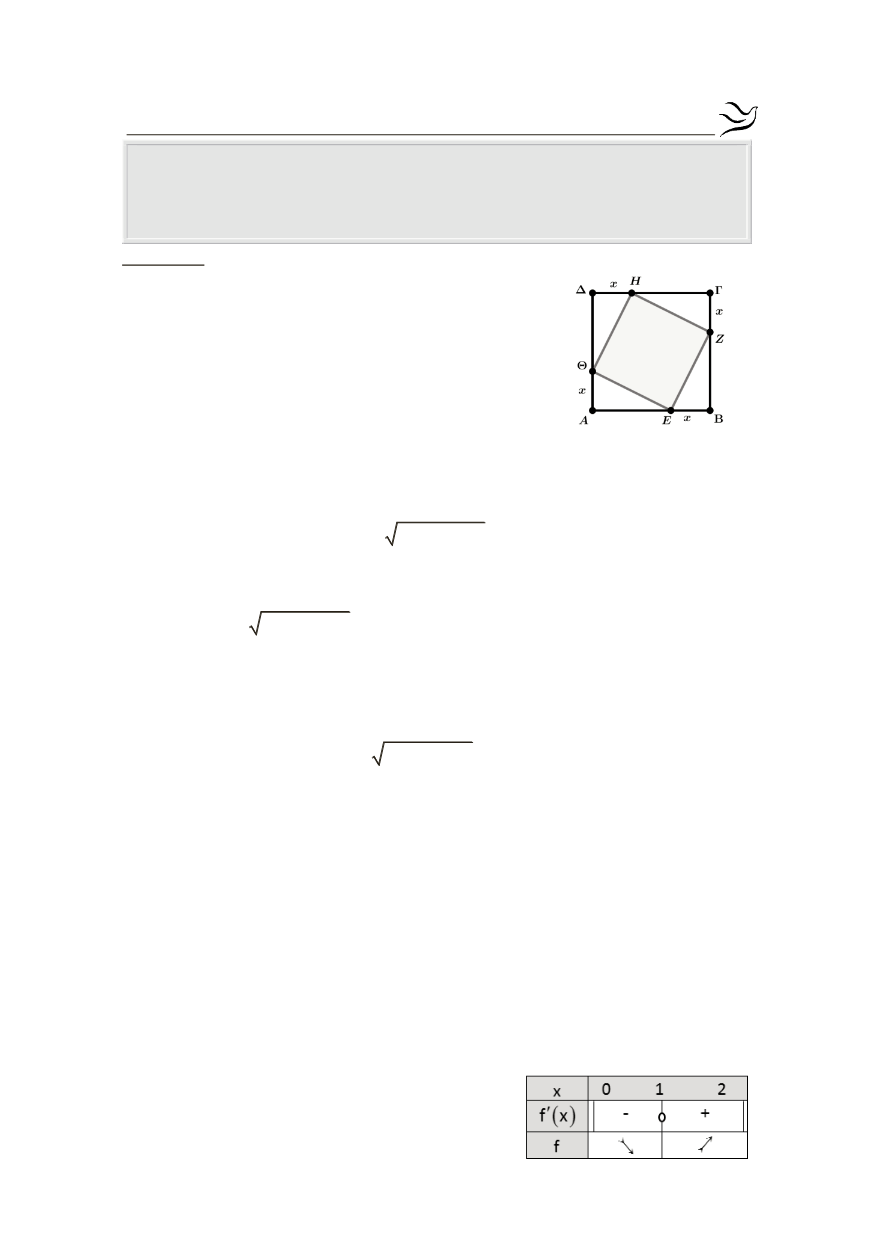
Β1.
Είναι
=
ΒΓ 2
άρα
= - Û = -
ΖΒ ΒΓ ΖΓ ΖΒ 2 x
Στο ορθογώνιο τρίγωνο
EBZ
D
ισχύει Πυθαγόρειο
Θεώρημα
( ) ( ) ( )
( )
(
)
= + Û = + -
2
2
2
2
2
2
EZ EB BZ
EZ x 2 x
( )
Û = + - +
2 2
2
EZ x 4 4x x
( )
Û = - +
2
2
EZ 2x 4x 4
( )
Û = - +
2
EZ 2x 4x 4
Είναι
³
x 0
και
- ³ Û £
2 x 0 x 2
Άρα
( )
= - +
2
EZ 2x 4x 4
με
£ £
0 x 2
.
Β2.
Το εμβαδόν Ε του τετραγώνου ΕΖΗΘ είναι
( )
= = - + = - +
2
2
2
2
E EZ 2x 4x 4 2x 4x 4
Άρα η συνάρτηση
( )
f x
που εκφράζει το εμβαδόν του τετραγώνου ΕΖΗΘ είναι
( )
= - +
2
f x 2x 4x 4
,
£ £
0 x 2
.
Β3.
Η
f
είναι συνεχής στο
[ ]
0,2
ως πολυωνυμική.
Η
f
είναι παραγωγίσιμη στο
( )
0,2
με
( )
¢
= -
f x 4x 4
( )
¢
= Û - = Û = Û =
f x 0 4x 4 0 4x 4 x 1









