Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
128
P
αν
(
)
0 0
x x ,x δ
Î +
, τότε, λόγω της
( )
1
, θα είναι
( ) ( )
0
0
f x f x
0
x x
-
£
-
, οπότε
θα έχουμε
( )
( ) ( )
0
0
0
x x
0
f x f x
f x lim
0
x x
+
®
-
¢
=
£
-
( )
3
Έτσι, από τις
( )
2
και
( )
3
έχουμε
( )
0
f x 0
¢
=
.
Η απόδειξη για τοπικό ελάχιστο είναι ανάλογη.
Α2. α)
Ψ
β)
Πρέπει εκατέρωθεν του
0
x
να αλλάζει πρόσημο η
( )
¢¢
f x
.
Α3.
δ.
A4.
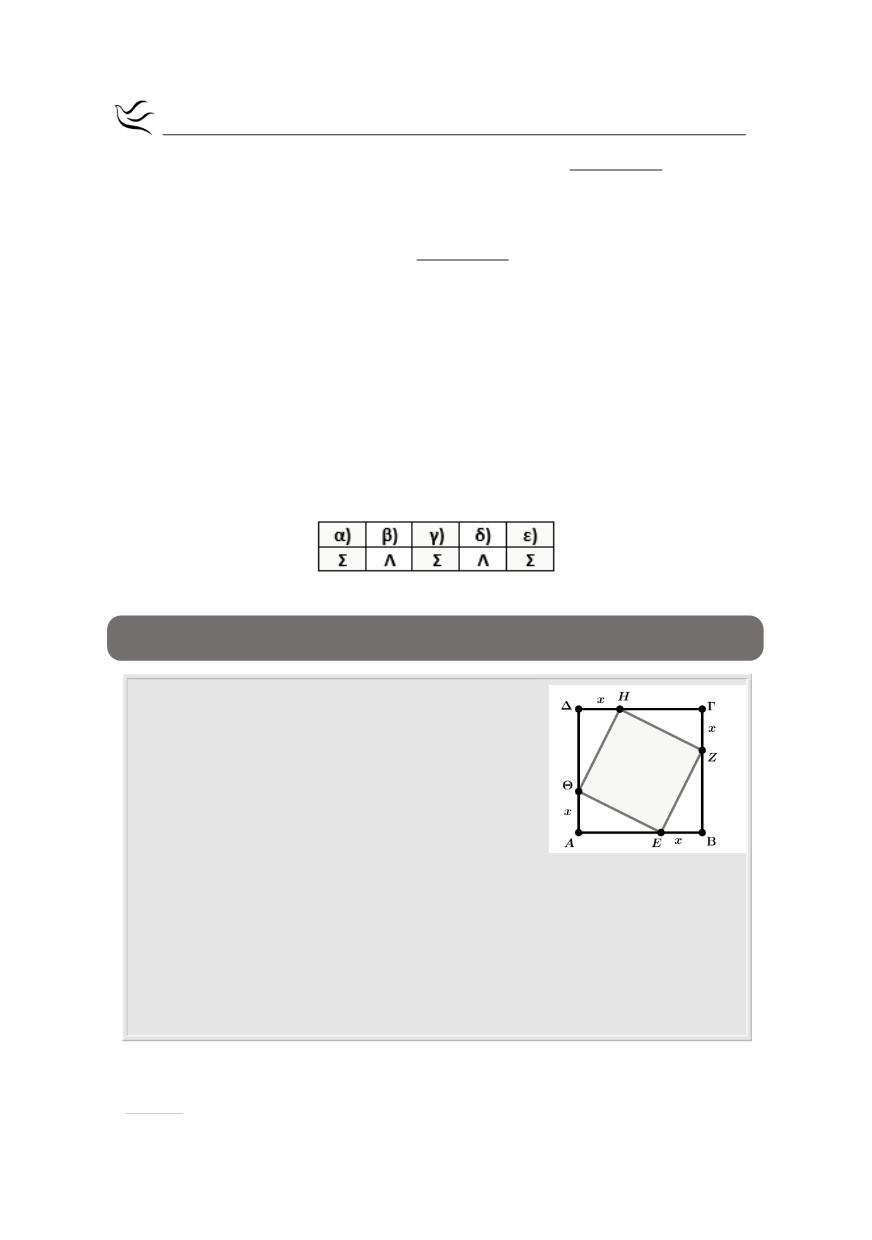
Δίνεται το τετράγωνο ΑΒΓΔ του διπλανού σχήμα-
τος με πλευρά 2
cm. A
ν το τετράγωνο ΕΖΗΘ έχει τις
κορυφές του στις πλευρές του ΑΒΓΔ
Β1.
Να εκφράσετε την πλευρά ΕΖ συναρτήσει του
x.
Μονάδες 6
Β2
. Να αποδείξετε ότι το εμβαδόν του τετραγώνου
ΕΖΗΘ δίνεται από τη συνάρτηση:
( )
2
f x 2x 4x 4
= - +
,
0 x 2
£ £
Μονάδες 4
Β3.
Να βρείτε για ποιες τιμές του
x
το εμβαδόν του τετραγώνου ΕΖΗΘ γίνεται
ελάχιστο και για ποιες μέγιστο.
Μονάδες 9
ΘΕΜΑ Β
ΕΠΑΝΑΛΗΠΤΙΚΕΣ ΕΞΕΤΑΣΕΙΣ 2017









