127
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
γ)
Αν ένα σημείο
( )
M α,β
ανήκει στη γραφική παράσταση μιας αντιστρέ-
ψιμης συνάρτησης
f,
τότε το σημείο
( )
M β,α
¢
ανήκει στη γραφική πα-
ράσταση
C
¢
της
1
f
-
.
δ)
Για κάθε συνεχή συνάρτηση
[ ]
f : α,β
®
, η οποία είναι παραγωγί-
σιμη στο
( )
α,β
, αν
( ) ( )
f α f β
=
τότε υπάρχει ακριβώς ένα
( )
ξ α,β
Î
τέτοιο ώστε
( )
f ξ 0
¢
=
.
ε)
Για κάθε συνεχή συνάρτηση
[ ]
f : α,β
®
, αν ισχύει
( )
α
β
f x dx 0
=
ò
τότε
( )
f x 0
=
για κάθε
[ ]
x α,β
Î
.
Μονάδες 10
A
πάντηση
Α1.
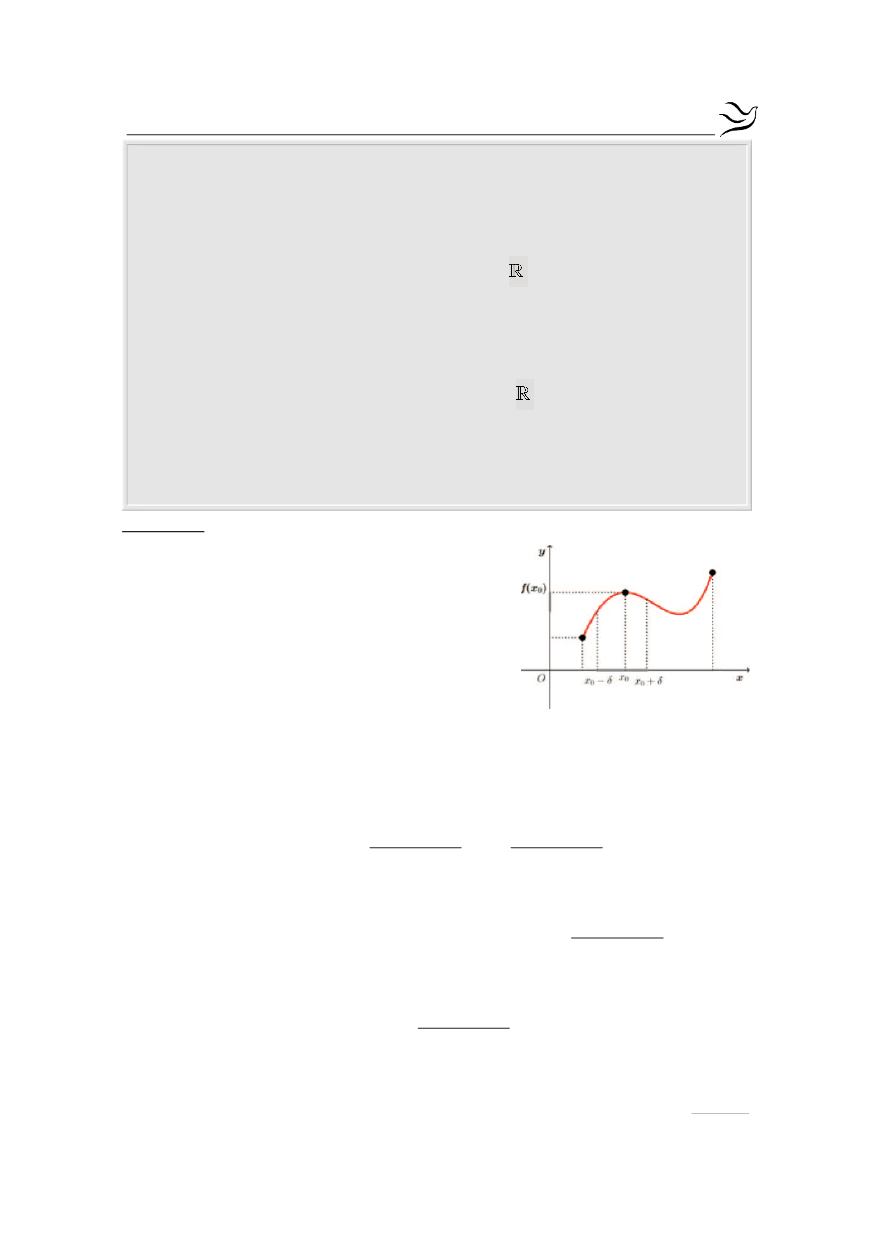
Ας υποθέσουμε ότι η f παρουσιάζει στο
0
x
τοπικό μέγιστο. Επειδή το
0
x
είναι εσωτε-
ρικό σημείο του Δ και η f παρουσιάζει σ’
αυτό τοπικό μέγιστο, υπάρχει
δ 0
>
τέτοιο,
ώστε
(
)
0
0
x δ,x δ Δ
- + Í
και
( ) ( )
0
f x f x
£
, για κάθε
(
)
0
0
x x δ,x δ
Î - +
. (1)
Επειδή, επιπλέον, η f είναι παραγωγίσιμη στο
0
x
, ισχύει
( )
( ) ( )
( ) ( )
0
0
0
0
0
x x
x x
0
0
f x f x
f x f x
f x lim
lim
x x
x x
-
+
®
®
-
-
¢
=
=
-
-
.
Επομένως,
P
αν
(
)
0
0
x x δ,x
Î -
, τότε, λόγω της
( )
1
, θα είναι
( ) ( )
0
0
f x f x
0
x x
-
³
-
, οπότε
θα έχουμε
( )
( ) ( )
0
0
0
x x
0
f x f x
f x lim
0
x x
-
®
-
¢
=
³
-
( )
2









