123
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
( )
3
4
f x
x 0
3
¢
= - - <
, άρα
[
]
f
στο 1,0
-
2
Σ
·
Στο
(
]
0,π
είναι:
( )
(
)
x
f x e ημx συνx
¢
= ×
+
, με
( )
3π
f x 0 x
4
¢
= Û =
.
Επιπλέον, η
f
¢
συνεχής στο
(
]
0,π
, άρα διατηρεί πρόσημο σε κάθε ένα
από τα διαστήματα
3π
0,
4
æ
ö
ç
÷
è
ø
,
3π
,π
4
æ
ù
ç
ú
è
û
.
Αφού
π
π
π
4
4
4
π
π π
2
f
e ημ συν e 2
2 e 0
4
4
4
2
æ ö
æ
ö
¢
= ×
+
= × ×
= ×
>
ç ÷
ç
÷
è ø
è
ø
είναι
( )
f x 0
¢
>
στο
3π
0,
4
æ
ö
ç
÷
è
ø
, οπότε
3π
f στο 0,
4
é
ù
ê
ú
ë
û
1
.
Επιπλέον,
( )
(
)
π
π
f π e ημπ συνπ e 0
¢
= ×
+ = - <
, άρα
( )
f x 0
¢
<
στο διά-
στημα
3π
,π
4
æ
ù
ç
ú
è
û
δηλαδή
3π
f στο
,π
4
é
ù
ê
ú
ë
û
2
.
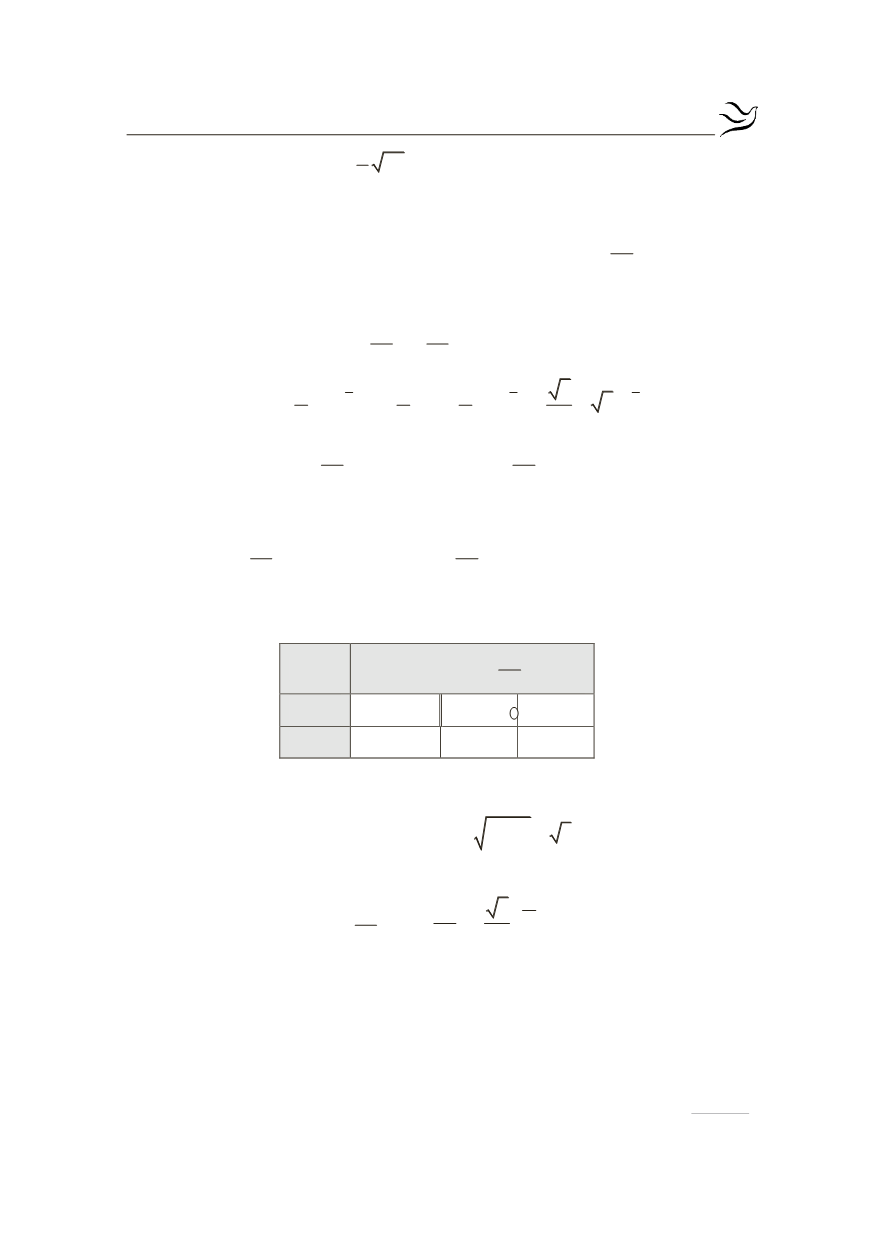
Ακολουθεί ο πίνακας μεταβολών για τη συνάρτηση
f:
x
3π
1 0
π
4
-
( )
f x
¢
-
+
-
f
2
1
2
Η συνάρτηση παρουσιάζει:
·
τοπικό μέγιστο στο
x 1
=-
, το
( ) ( )
4 3
3
f 1
1 1 1
- = - = =
·
τοπικό ελάχιστο στο
x 0
=
, το
( )
f 0 0
=
·
τοπικό μέγιστο στο
3π
x
4
=
, το
3π
4
3π 2
f
e
4 2
æ ö = ç ÷
è ø
·
τοπικό ελάχιστο στο
x π
=
, το
( )
π
f π e ημπ 0
= ×
=
Για το σύνολο τιμών:
·
Στο διάστημα
[
]
1,π
-
η συνάρτηση είναι συνεχής, επομένως παρουσιάζει
μια μέγιστη Μ και μία ελάχιστη τιμή
m.









