Μαθηματικά Γ' Λυκείου

119 / 368

Εκδόσεις ΜΠΑΧΑΡΑΚΗ – Μαθηματικά Προσανατολισμού
118
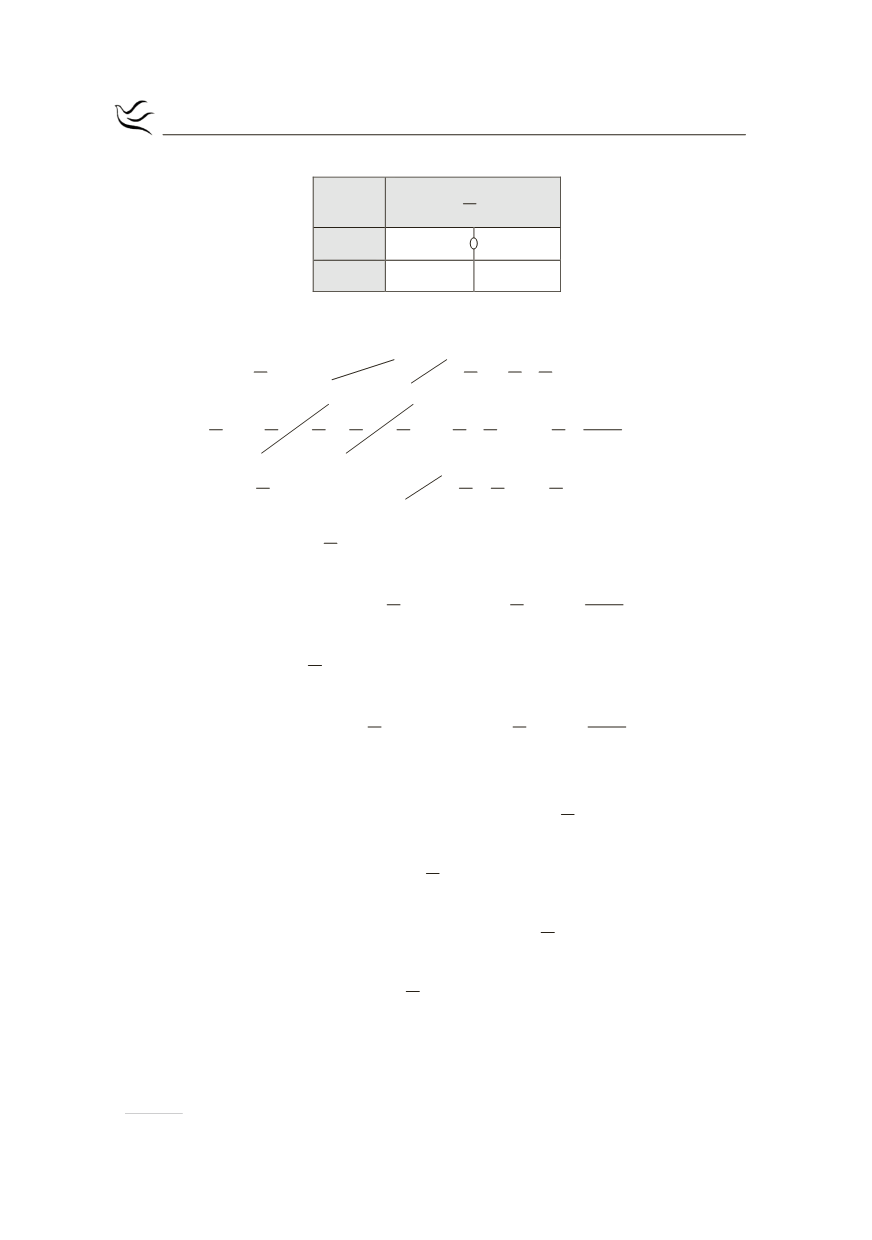
Ακολουθεί ο πίνακας μεταβολών για τη συνάρτηση g:
x
π
0 π
2
( )
g x¢ + -
g 1 2
Είναι:
· ( ) π
g 0 συν0 0 συν0
2
= - × + × ημ0 - π π π
0
2 2 2
+ = - + =
·
π π π
g συν
2 2 2
æ ö = - ç ÷
è ø
π π
συν
2 2
+ π π π π 2
ημ 1
2 2 2 2
-
- + = - + =
· ( ) π
g π συνπ π συνπ ημπ
2
= - + × -
π π π
π 0
2 2 2
+ = - + =
· Στο διάστημα
π
0,
2
é ù
ê ú ë û η g είναι συνεχής και γνησίως αύξουσα, συνεπώς:
( )
1
π π π 2
Δ g 0, g 0 ,g 0,
2 2 2
æ ö é ù - é ù æ ö é ù
= = =
ç ÷ ç ÷ ê ú ê ú ê ú
ë û è ø ë û è ø ë û
· Στο διάστημα
π
,π
2
é ù
ê ú ë û η g είναι συνεχής και γνησίως φθίνουσα, άρα:
( )
2
π π π 2
Δ g ,π g π ,g 0,
2 2 2
æ ö é ù - é ù æ ö é ù
= = =
ç ÷ ç ÷ ê ú ê ú ê ú
ë û è ø ë û è ø ë û
Συνεπώς:
· 1 0 ΔÎ και η g είναι γνησίως μονότονη στο
π
0,
2
é ù
ê ú ë û , άρα υπάρχει μονα-
δική ρίζα της ( )
g x 0= στο
π
0,
2
é ù
ê ú ë û, η οποία μάλιστα είναι το 0.
· 2 0 ΔÎ και η g είναι γνησίως μονότονη στο
π
,π
2
é ù
ê ú ë û , άρα υπάρχει μονα-
δική ρίζα της ( )
g x 0= στο
π
,π
2
é ù
ê ú ë û , η οποία μάλιστα είναι το π .
Δηλαδή, ( )
g x 0 x 0 ή x π= Û = = .
Τότε οι εξισώσεις των ζητούμενων εφαπτομένων είναι: