119
Μαθηματικά Προσανατολισμού– Εκδόσεις ΜΠΑΧΑΡΑΚΗ
·
( )
1
ε : y x συν0 0 συν0 ημ0 y x
= - ×
+ ×
- Û = -
·
( )
2
ε : y x συνπ π συνπ ημπ y x π
= - ×
+ ×
- Û = -
Γ2.
Είναι:
( )
f x ημx
¢¢
=
,
[ ]
x 0,π
Î
Μάλιστα, στο
[ ]
0,π
είναι
( )
ημx 0 f x 0
¢¢
³ Û ³
, με την ισότητα να ισχύει μόνο
για
x 0
=
και
x π
=
, άρα η
f
είναι κυρτή στο
[ ]
f
D 0,π
=
. Τότε, η
f
C
θα βρίσκε-
ται πάνω από τις
( )
1
ε
και
( )
2
ε
, με εξαίρεση τα σημεία επαφής
( )
1
M 0,0
και
( )
2
M π,0
. Επιπλέον, στο
[ ]
0,π
ισχύει:
( )
ημx 0 ημx 0 f x 0
³ Û- £ Û £
, άρα η
f
C
βρίσκεται κάτω από τον άξονα
x x
¢
στο
( )
0, π
και τον τέμνει στο
x 0
=
και
x π
=
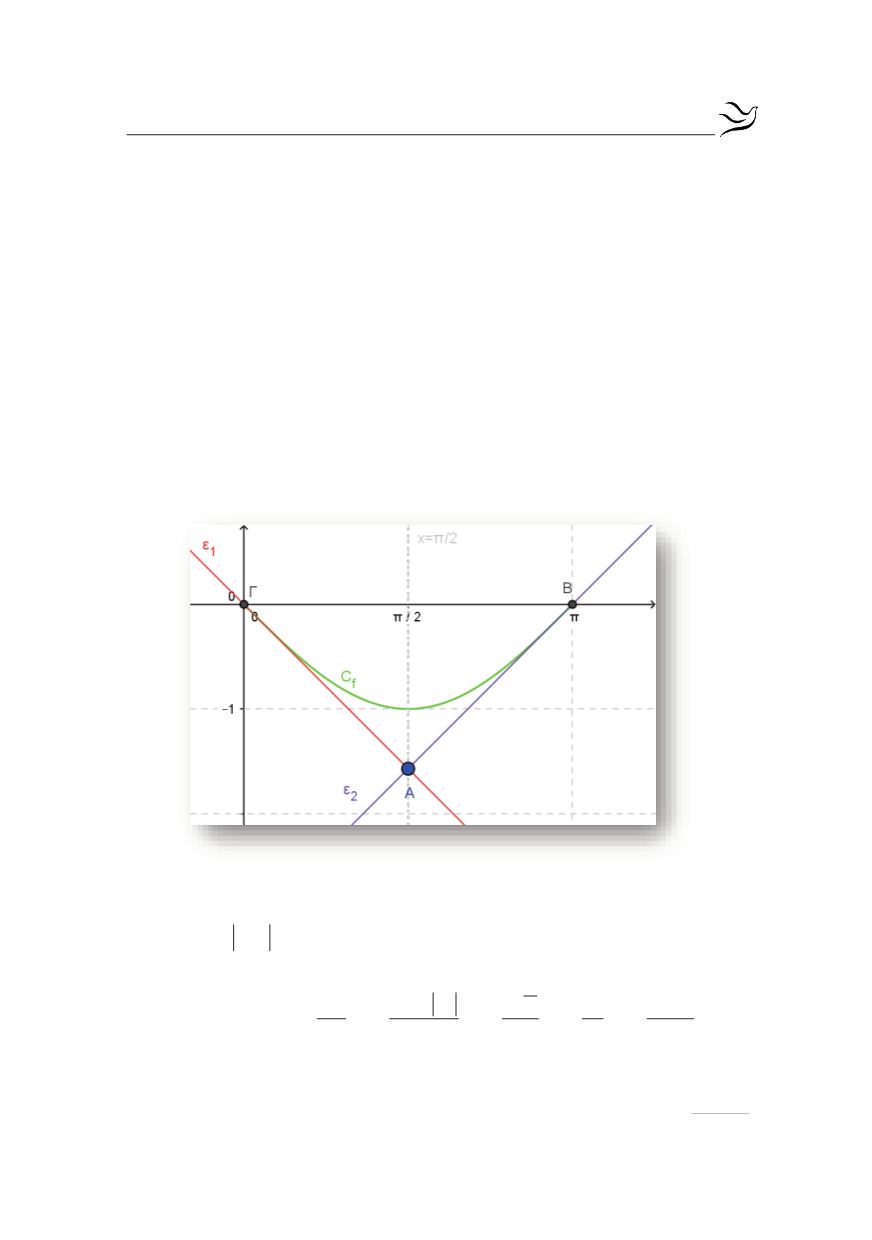
. Ακολουθούν οι γραφικές παραστάσεις:
Ας είναι:
·
( )
(
)
[
]
π
π
π
π
2
0
0
0
0
E f x dx
ημx dx ημxdx συνx
συνπ συν0 2
=
= - -
=
= -
= - + =
ò
ò
ò
·
(
)
( )
2
2
A
1
2
π
π
ΒΓ y
β υ
π π 8
2
E ΑΒΓ Ε
2
2
2
2
2
2
2
4
4
×
×
×
-
= - = - =
- = - = - =
Τότε:









