Τράπεζα Θεμάτων Γεωμετρίας Α’ Γενικού Λυκείου – Εκδόσεις ΜΠΑΧΑΡΑΚΗ
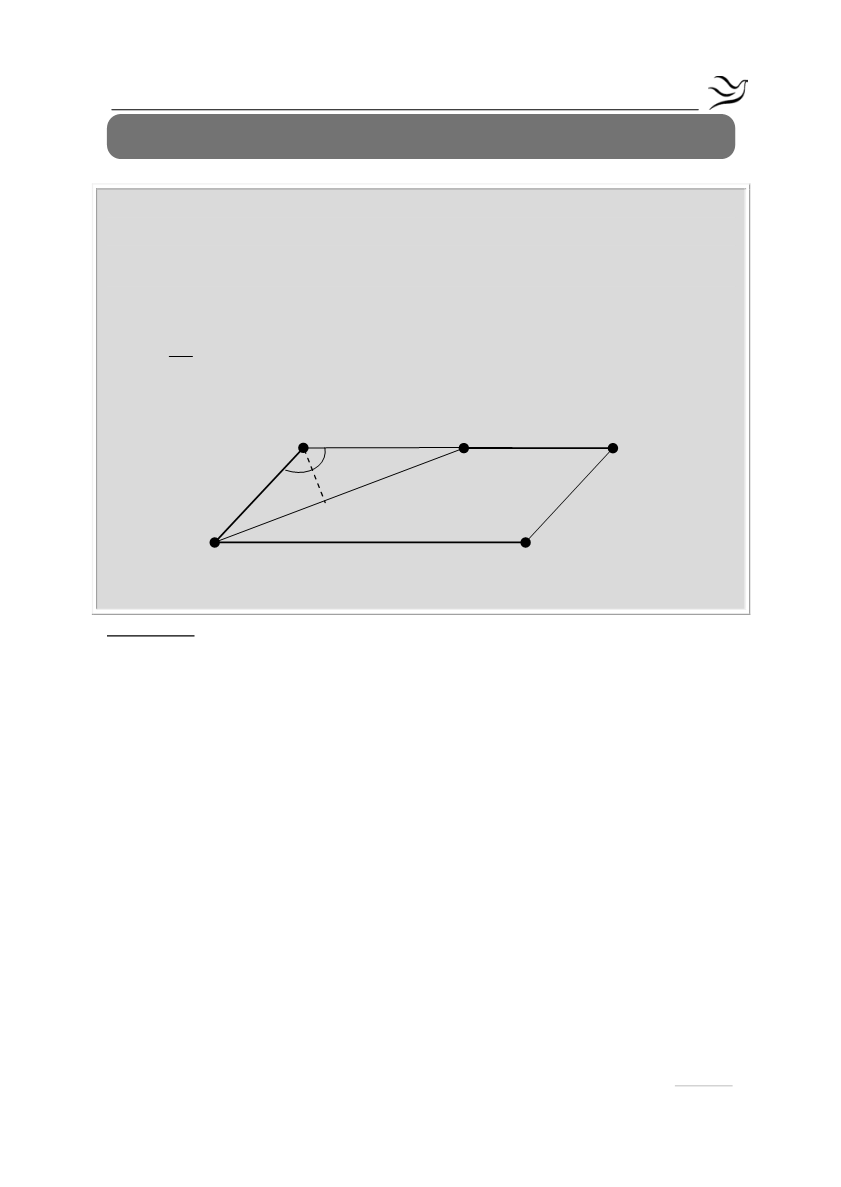
Δίνεται παραλληλόγραμμο ΑΒΓΔ με γωνία
0
Α 120
=
και ΑΒ=2ΑΔ. Φέρουμε τη
διχοτόμο της γωνίας
Δ
του παραλληλογράμμου, η οποία τέμνει την ΑΒ στο Ε,
και στη συνέχεια το κάθετο τμήμα ΑΖ στη ΔΕ. Να αποδείξετε ότι:
α)
0
ΑΔΕ 30
=
(Μονάδες 12)
β)
ΑΒ ΑΖ
4
=
. (Μονάδες 13)
Απάντηση:
α) Η ΔΕ είναι τέμνουσα των παραλλήλων ΑΕ και ΔΓ άρα,
ΑΕΔ ΕΔΓ
=
(1)
ως εντός εναλλάξ.
Επιπλέον, από τα δεδομένα
ΑΔΕ ΕΔΓ
=
(2)
οπότε από τις σχέσεις (1) και (2) συμπεραίνουμε ότι
ΑΕΔ ΑΔΕ
=
.
Συνεπώς, στο τρίγωνο ΑΔΕ είναι
0
Α ΑΔΕ ΔΑΕ 180
+ + = ⇔
0
0
120 2ΑΔΕ 180
+ = ⇔
0
2ΑΔΕ 60
= ⇔
0
ΑΔΕ 30
=
.
Α
Β
Δ
●
Ε
Γ
Ζ
ΘΕΜΑ2844
49









